Lecture 8 Discrete random variables
Learning objectives
- Define random variables
- Distinguish between discrete and interval variables
- Identify discrete random variable distributions relevant to social science
- Review measures of central tendency and dispersion
- Define expected value and variance
- Define cumulative mass functions (CMFs) for discrete random variables
Supplemental readings
- Chapter 2.1-.4, Bertsekas and Tsitsiklis (2008)
- Equivalent reading from Bertsekas and Tsitsiklis lecture notes
8.1 Random variable
A random variable is a random process or variable with a numerical outcome. More formally, it is a random variable \(X\) that is a function of the sample space
- Number of incumbents who win
- An indicator whether a country defaults on a loan (1 if a default, 0 otherwise)
- Number of casualties in a war (rather than all possible outcomes)
\[X:\text{Sample Space} \rightarrow \Re\]
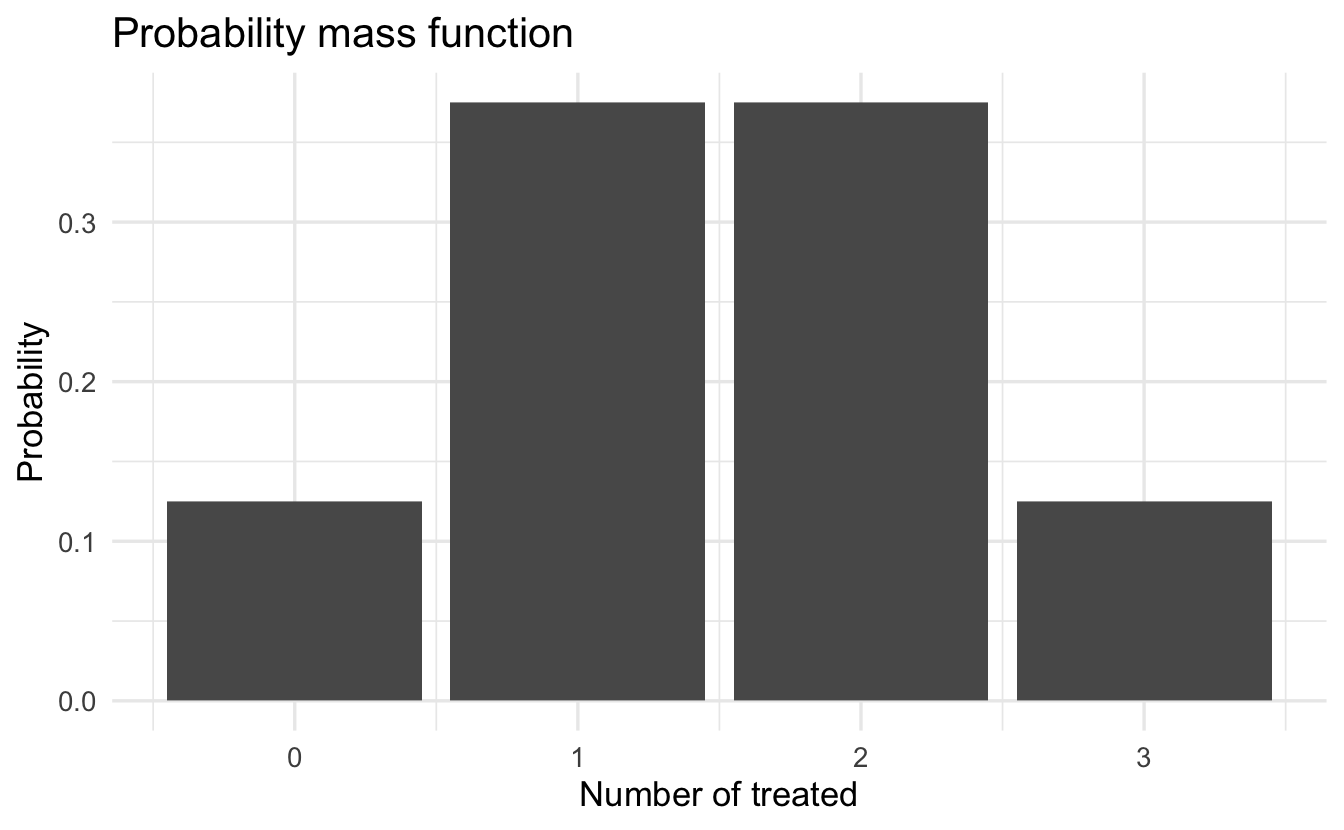
Example 8.1 (Treatment assignment) Suppose we have \(3\) units, flipping fair coin (\(\frac{1}{2}\)) to assign each unit. Assign to \(T=\)Treatment or \(C=\)control, with \(X\) = Number of units received treatment. The function is
\[ X = \left \{ \begin{array} {ll} 0 \text{ if } (C, C, C) \\ 1 \text{ if } (T, C, C) \text{ or } (C, T, C) \text{ or } (C, C, T) \\ 2 \text{ if } (T, T, C) \text{ or } (T, C, T) \text{ or } (C, T, T) \\ 3 \text{ if } (T, T, T) \end{array} \right. \]
In other words:
\[ \begin{aligned} X( (C, C, C) ) & = 0 \\ X( (T, C, C)) & = 1 \\ X((T, C, T)) & = 2 \\ X((T, T, T)) & = 3 \end{aligned} \]
Example 8.2 (Legislative calls) \(X\) = Number of Calls into congressional office in some period \(p\)
\[X(c) = c\]
Example 8.3 (Electoral outcome) Define \(v\) as the proportion of vote the candidate receives. \(X = 1\) if \(v>0.50\), while \(X = 0\) if \(v<0.50\). For example, if \(v = 0.48\), then \(X(v) = 0\).
Example 8.4 (Loan default) An indicator whether a country defaults on a loan (1 if a default, 0 otherwise)
Not all random variables are the result of an experiment - most are observational.
8.2 Probability mass functions
A probability mass function (PMF) defines the probability of the values that a discrete random variable can take.
8.2.1 Intuition
Go back to our experiment example – probability comes from probability of outcomes
\[\Pr(C, T, C) = \Pr(C)\Pr(T)\Pr(C) = \frac{1}{2}\frac{1}{2}\frac{1}{2} = \frac{1}{8}\]
This applies to all outcomes:
\[ \begin{aligned} p(X = 0) & = \Pr(C, C, C) = \frac{1}{8}\\ p(X = 1) & = \Pr(T, C, C) + \Pr(C, T, C) + \Pr(C, C, T) = \frac{3}{8} \\ p(X = 2) & = \Pr(T, T, C) + \Pr(T, C, T) + \Pr(C, T, T) = \frac{3}{8} \\ p(X = 3) & = \Pr(T, T, T) = \frac{1}{8} \\ p(X = a) &= 0 \, \forall \, a \notin (0, 1, 2, 3) \end{aligned} \]
8.2.2 Definition
Definition 8.1 (Probability mass function) For a discrete random variable \(X\), define the probability mass function \(p_X(x)\) as
\[p_X(x) = \Pr(X = x)\]
Use upper-case letters to denote random variables, and lower-case letters to denote real numbers such as the numerical values of a random variable. Note that
\[\sum_x p_{X}(x) = 1\]
\(x\) ranges over all possible values of \(X\) which makes sense - probability must sum to 1.
We can also add probabilities for smaller sets \(S\) of possible values of \(X \in S\).
\[\Pr(X \in S) = \sum_{x \in S} p_X (x)\]
For example, if \(X\) is the number of heads obtained in two independent tosses of a fair coin, the probability of at least one head is
\[\Pr (X > 0) = \sum_{x=1}^2 p_X (x) = \frac{1}{2} + \frac{1}{4} = \frac{3}{4}\]
To calculate the PMF of a random variable \(X\)
- For each possible value \(x\) of \(X\)
- Collect all possible outcomes that give rise to the event \(\{ X=x \}\)
- Add their probabilities to obtain \(p_X (x)\)
Example 8.5 (Topic models) Topics are distinct concepts (war in Afghanistan, national debt, fire department grants) found in a corpus of text documents. Mathematically they are probability mass functions on Words (probability of using word, when discussing a topic).
Suppose we have a set of words:
(afghanistan, fire, department, soldier, troop, war, grant)
Topic 1 (war)
- \(\Pr(\text{afghanistan}) = 0.3\); \(\Pr(\text{fire}) = 0.0001\); \(\Pr(\text{department}) = 0.0001\); \(\Pr(\text{soldier}) = 0.2\); \(\Pr(\text{troop}) = 0.2\); \(\Pr(\text{war})=0.2997\); \(\Pr(\text{grant})=0.0001\)
Topic 2 (fire departments):
- \(\Pr(\text{afghanistan}) = 0.0001\); \(\Pr(\text{fire}) = 0.3\); \(\Pr(\text{department}) = 0.2\); \(\Pr(\text{soldier}) = 0.0001\); \(\Pr(\text{troop}) = 0.0001\); \(\Pr(\text{war})=0.0001\); \(\Pr(\text{grant})=0.2997\)
Topic models take a set of documents and estimate topics.
8.3 Cumulative mass function
Definition 8.2 (Cumulative mass function) For a random variable \(X\), define the cumulative mass function \(F(x)\) as,
\[F(x) = \Pr(X \leq x)\]
The CMF characterizes how probability cumulates as \(X\) gets larger. \(F(x) \in [0,1]\), and \(F(x)\) is non-decreasing.
8.3.1 Three person experiment
Consider the three person experiment: \(\Pr(T) = \Pr(C) = 1/2\). What is \(F(2)\)?
\[ \begin{aligned} F(2) & = \Pr(X = 0) + \Pr(X = 1) + \Pr(X = 2) \\ & = \frac{1}{8} + \frac{3}{8} + \frac{3}{8} \\ & = \frac{7}{8} \end{aligned} \]
What is \(F(2) - F(1)\)?
\[ \begin{aligned} F(2) - F(1) & = [\Pr(X = 0) + \Pr(X = 1) + \Pr(X = 2)] \nonumber \\ & \quad -[\Pr(X = 0) + \Pr(X = 1)] \\ F(2) - F(1) & = \Pr(X = 2) \end{aligned} \]
There is a close relationship between PMFs and CMFs.
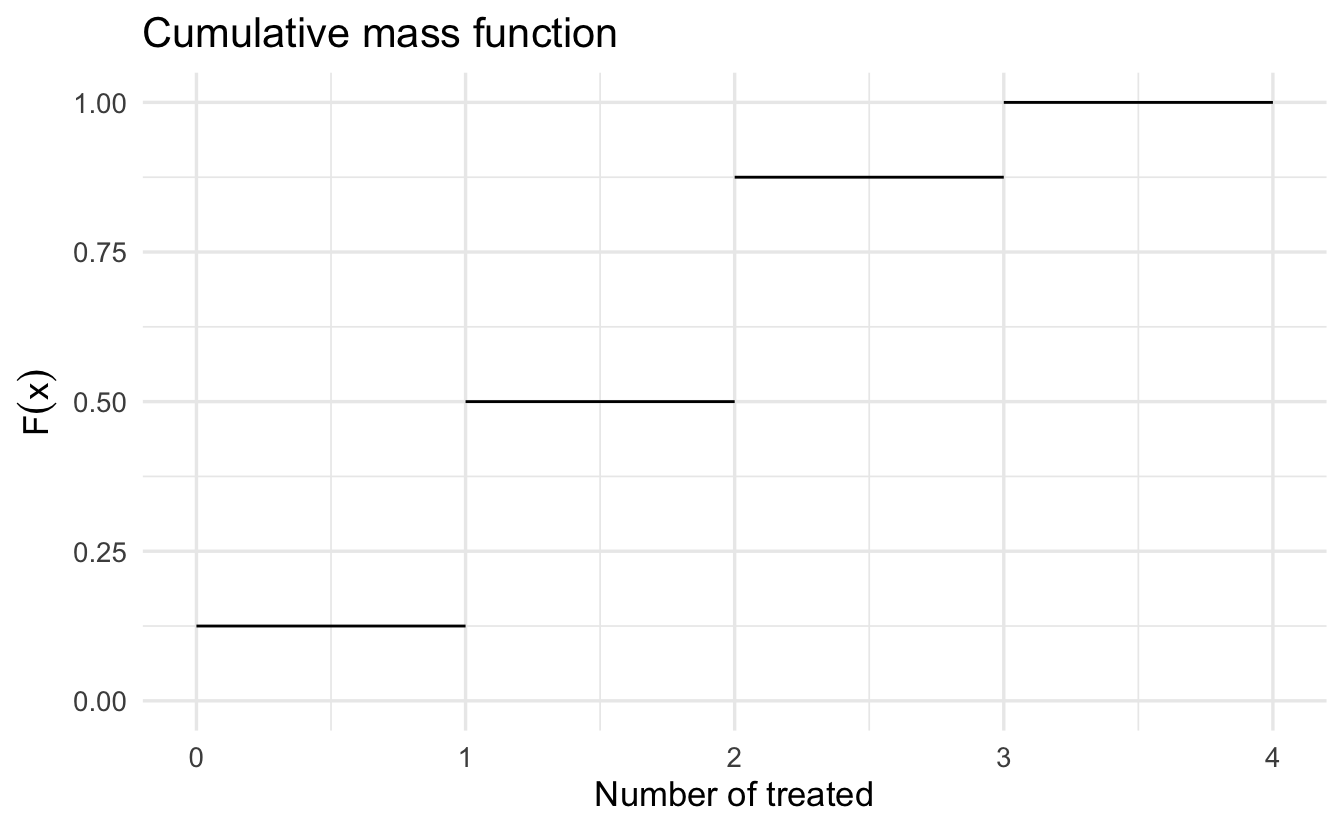
Cumulative functions are similar to integration, but over a discrete set of values.
8.4 Famous discrete random variables
8.4.1 Bernoulli
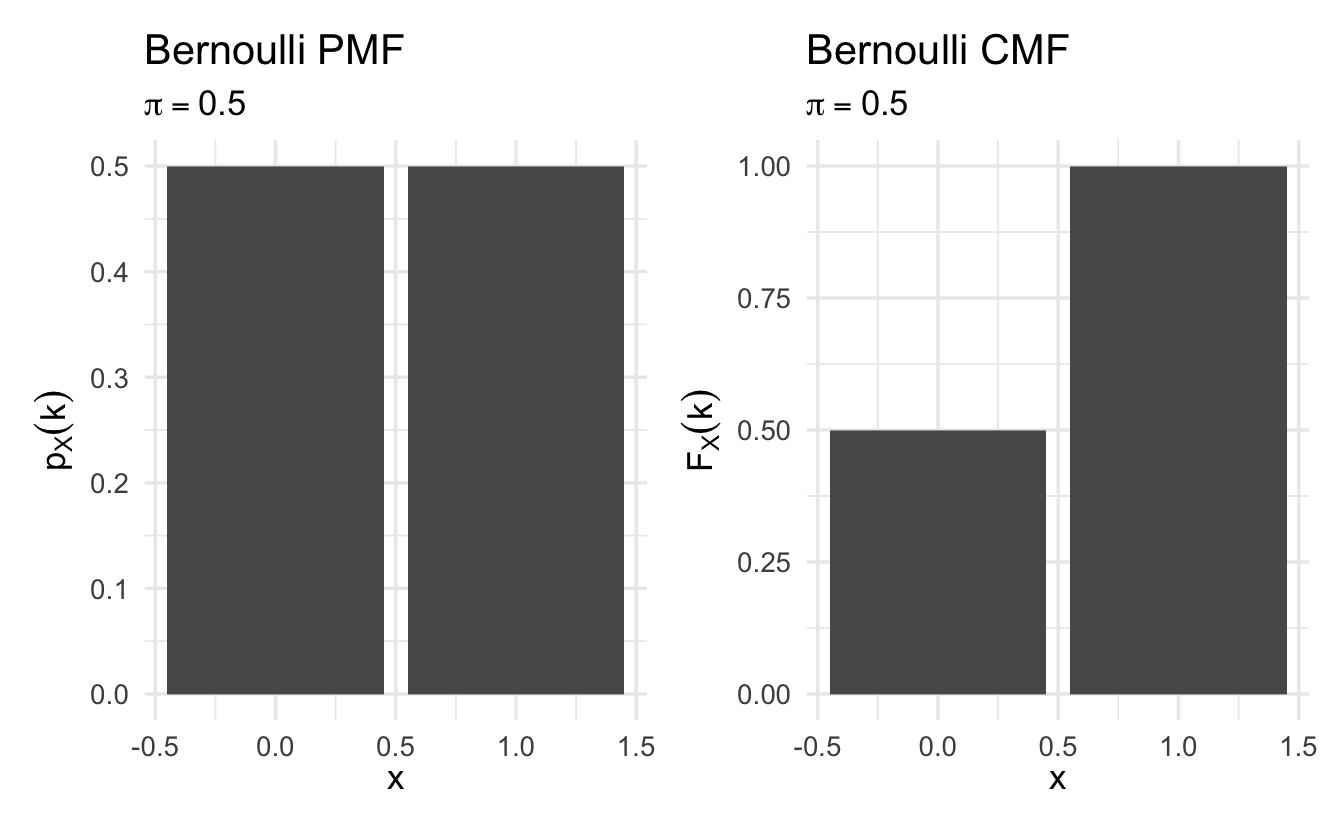
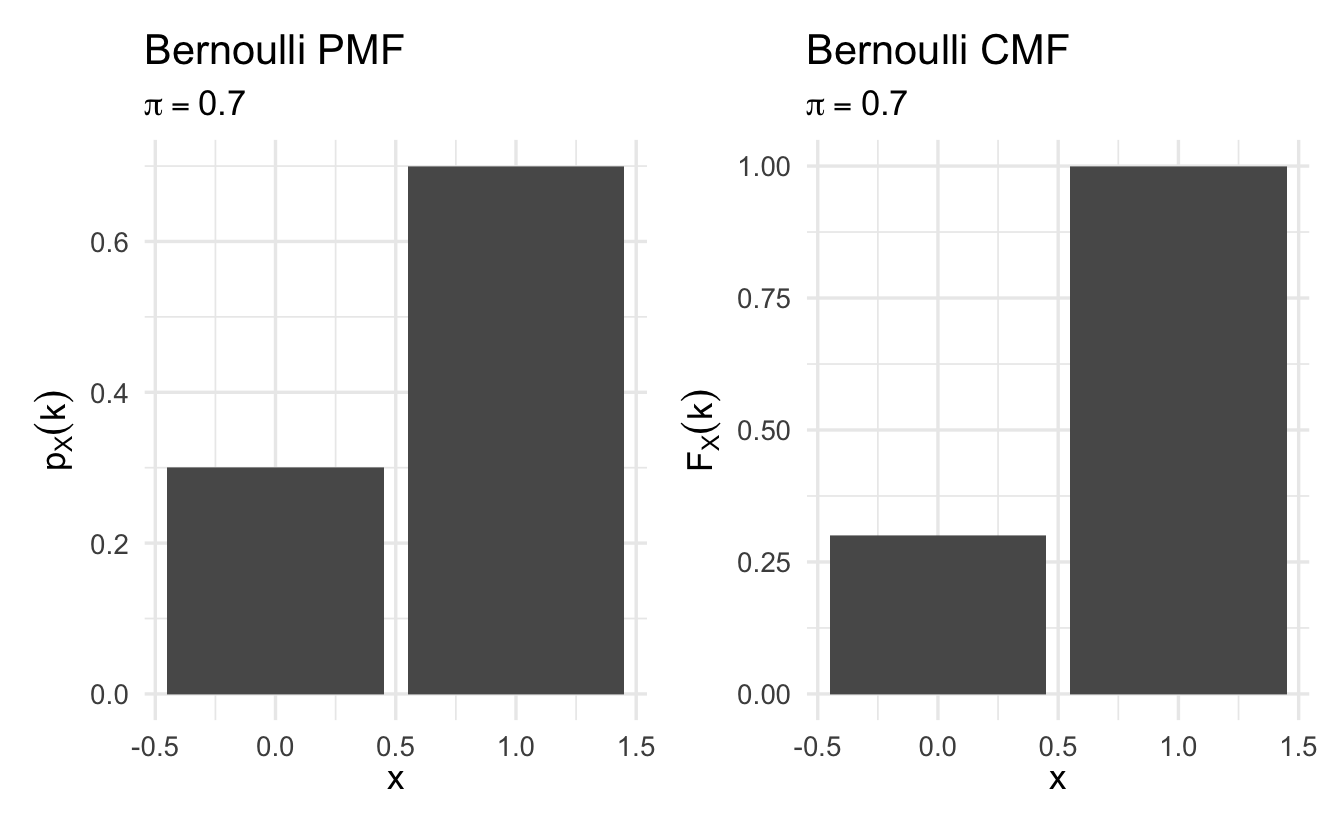
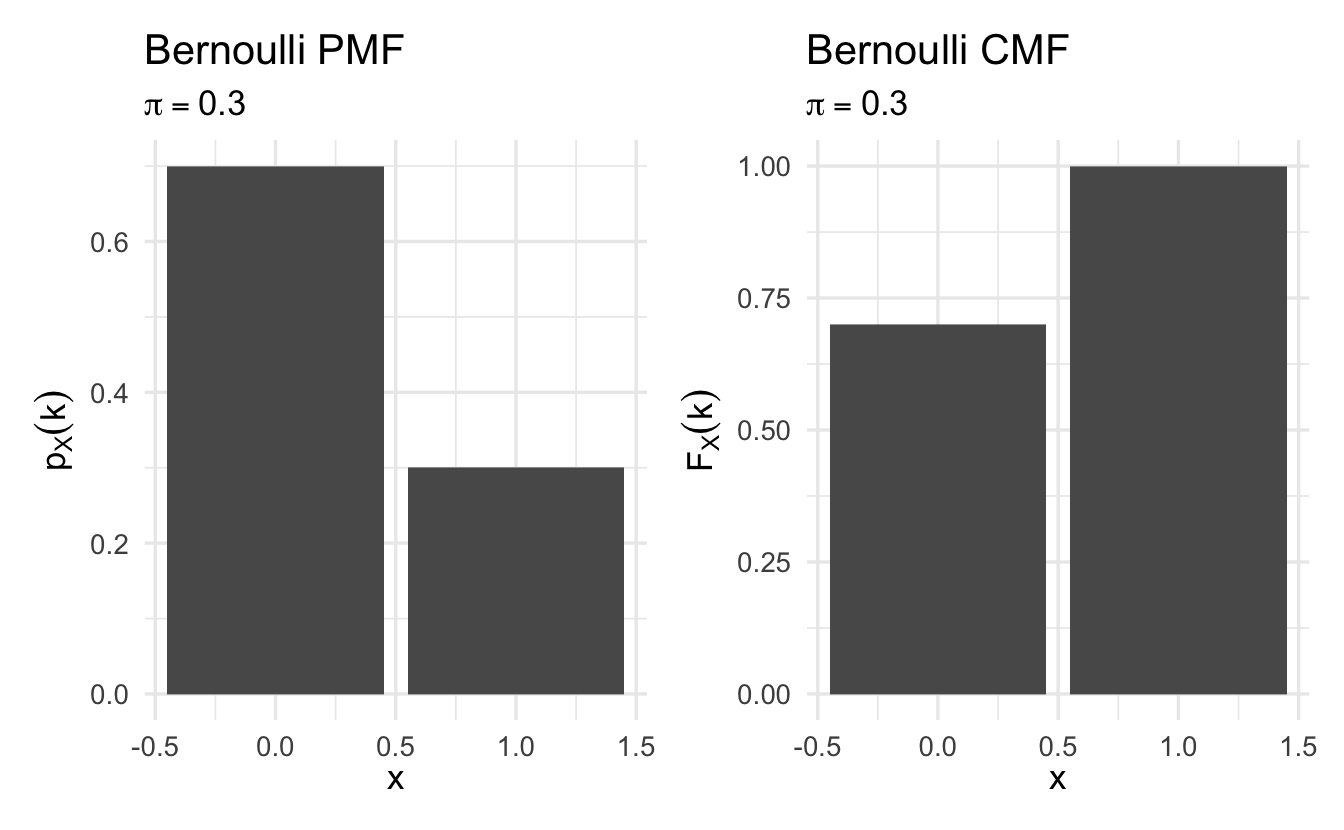
Definition 8.3 (Bernoulli random variable) Suppose \(X\) is a random variable, with \(X \in \{0, 1\}\) and \(\Pr(X = 1) = \pi\). Then we will say that \(X\) is Bernoulli random variable,
\[p_X(k)= \pi^{k} (1- \pi)^{1 - k}\]
for \(k \in \{0,1\}\) and \(p_X(k) = 0\) otherwise.
We will (equivalently) say that
\[Y \sim \text{Bernoulli}(\pi)\]
Suppose we flip a fair coin and \(Y = 1\) if the outcome is Heads.
\[ \begin{aligned} Y & \sim \text{Bernoulli}(1/2) \nonumber \\ p_X(1) & = (1/2)^{1} (1- 1/2)^{ 1- 1} = 1/2 \nonumber \\ p_X(0) & = (1/2)^{0} (1- 1/2)^{1 - 0} = (1- 1/2) \nonumber \end{aligned} \]
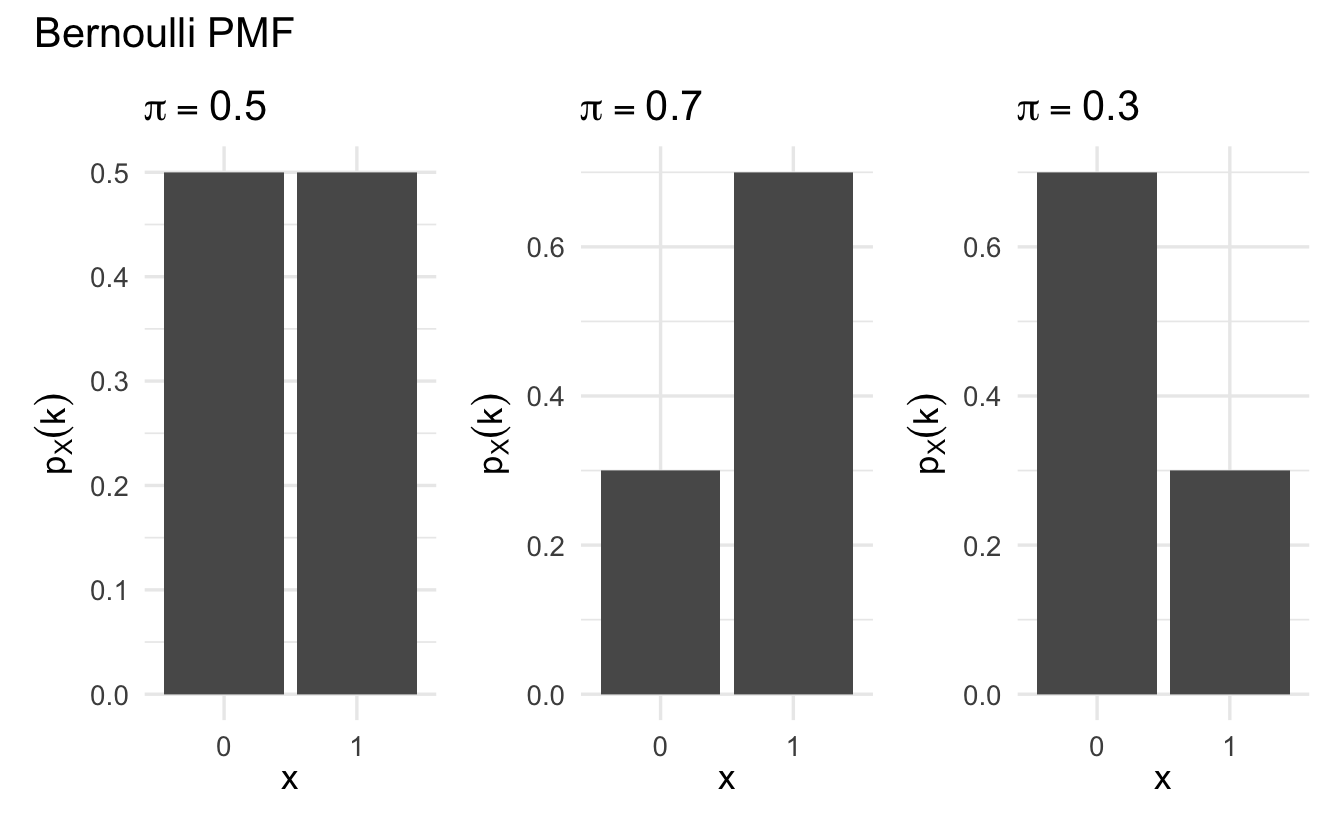
Figure 8.1: Example Bernoulli probability mass functions
Other examples include:
- Person is healthy or sick
- Person votes or does not vote
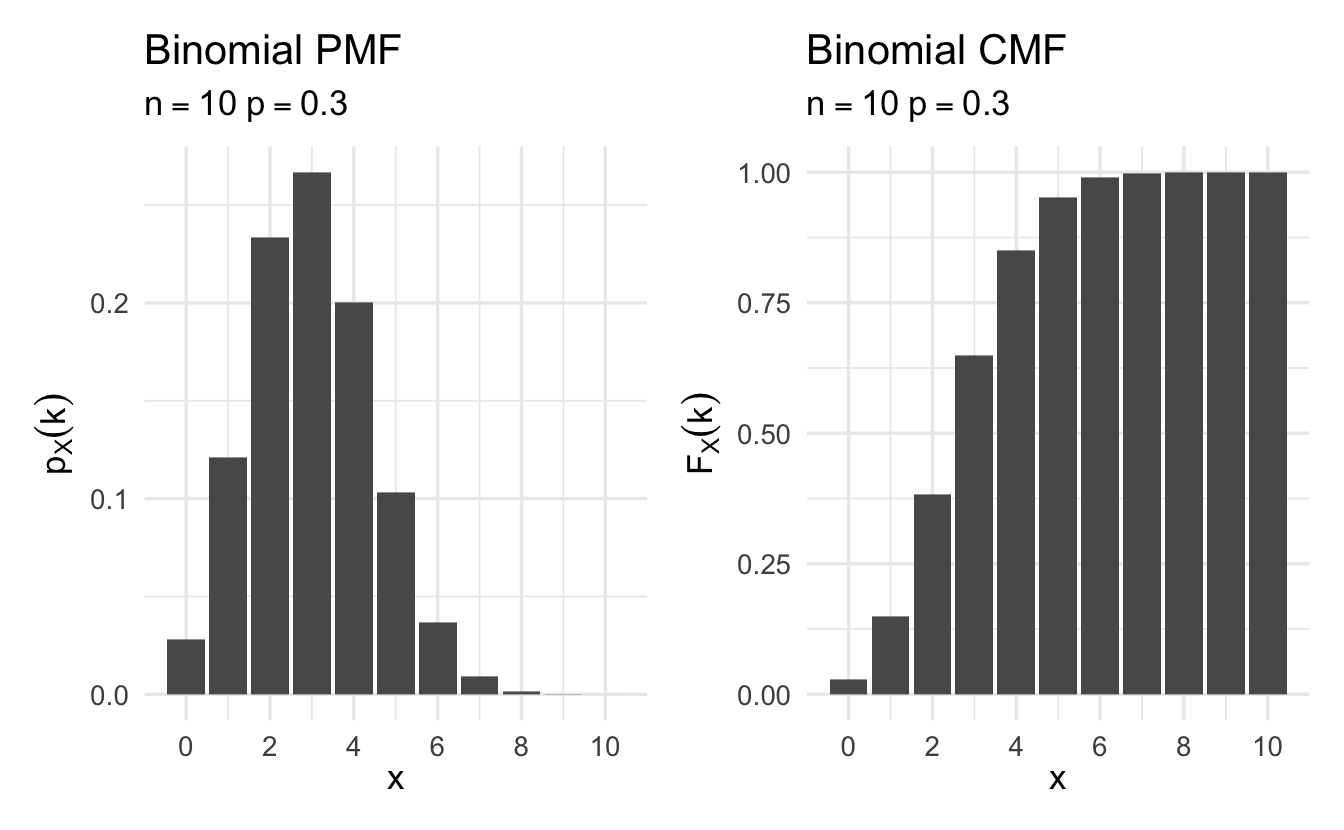
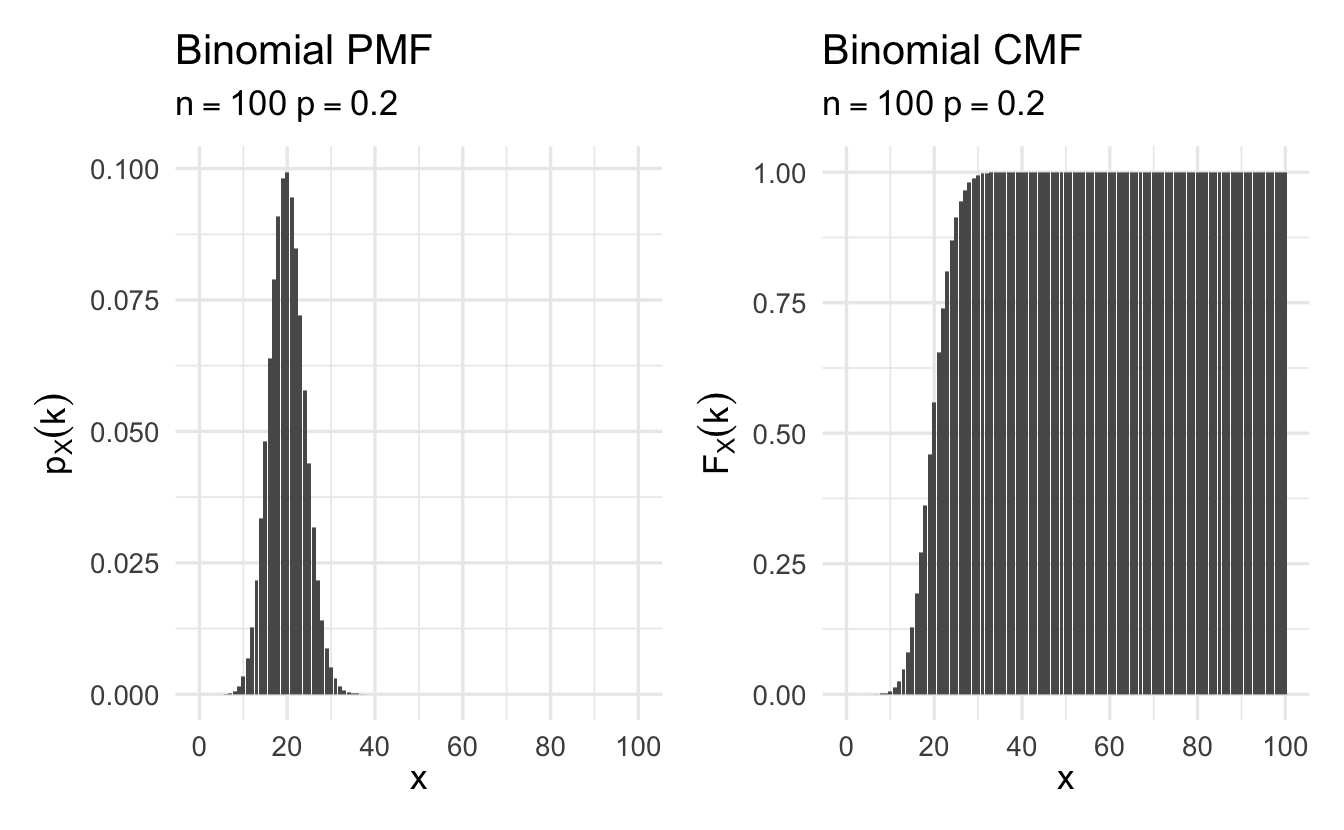
8.4.2 Binomial
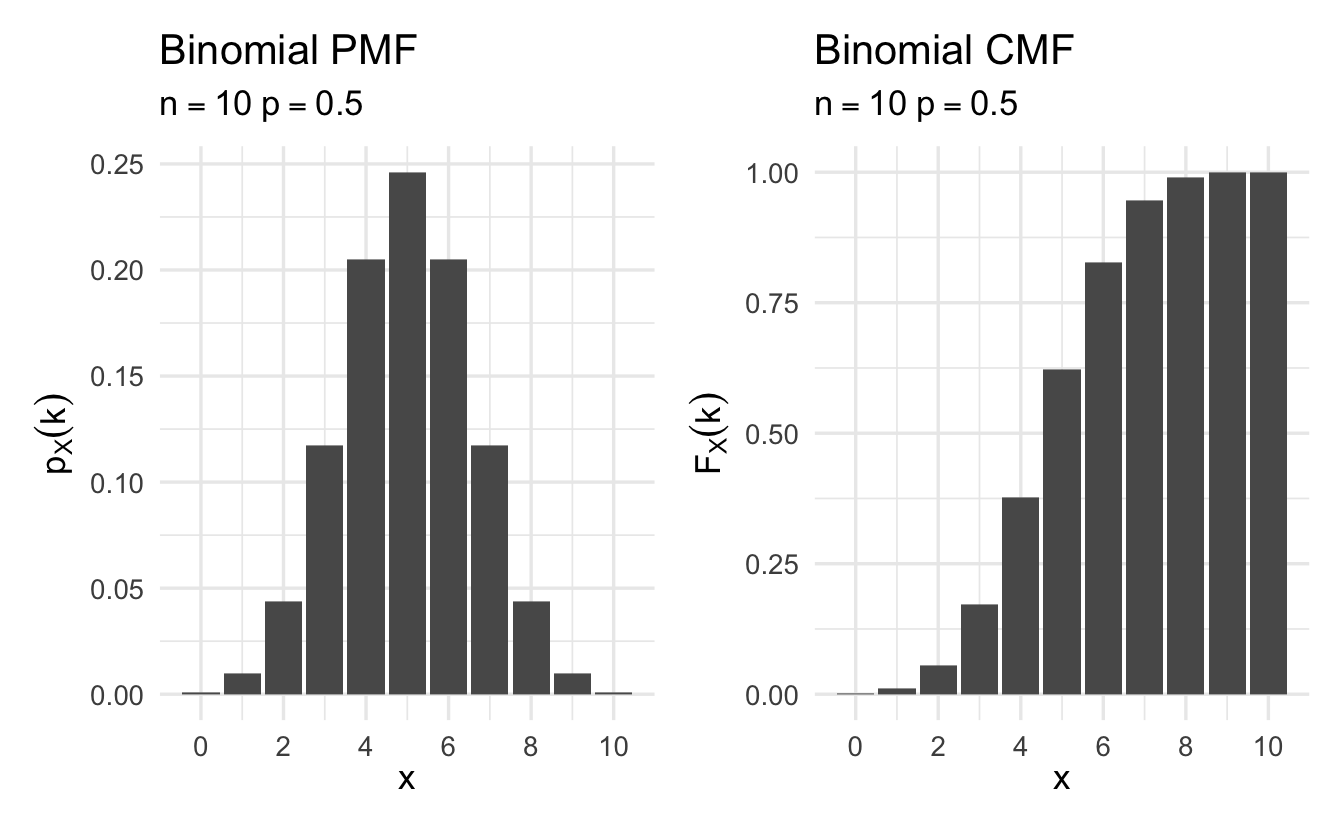
Definition 8.4 (Binomial random variable) Suppose \(X\) is a random variable that counts the number of successes in \(N\) independent and identically distributed Bernoulli trials. Then \(X\) is a Binomial random variable,
\[p_X(k) = {{N}\choose{k}}\pi^{k} (1- \pi)^{n-k}\]
for \(k \in \{0, 1, 2, \ldots, N\}\) and \(p_X(k) = 0\) otherwise, and \(\binom{N}{k} = \frac{N!}{(N-k)! k!}\). Equivalently,
\[Y \sim \text{Binomial}(N, \pi)\]
Binomial random variables can be used as a model to count the number of successes across \(N\) trials.
8.4.2.1 Example
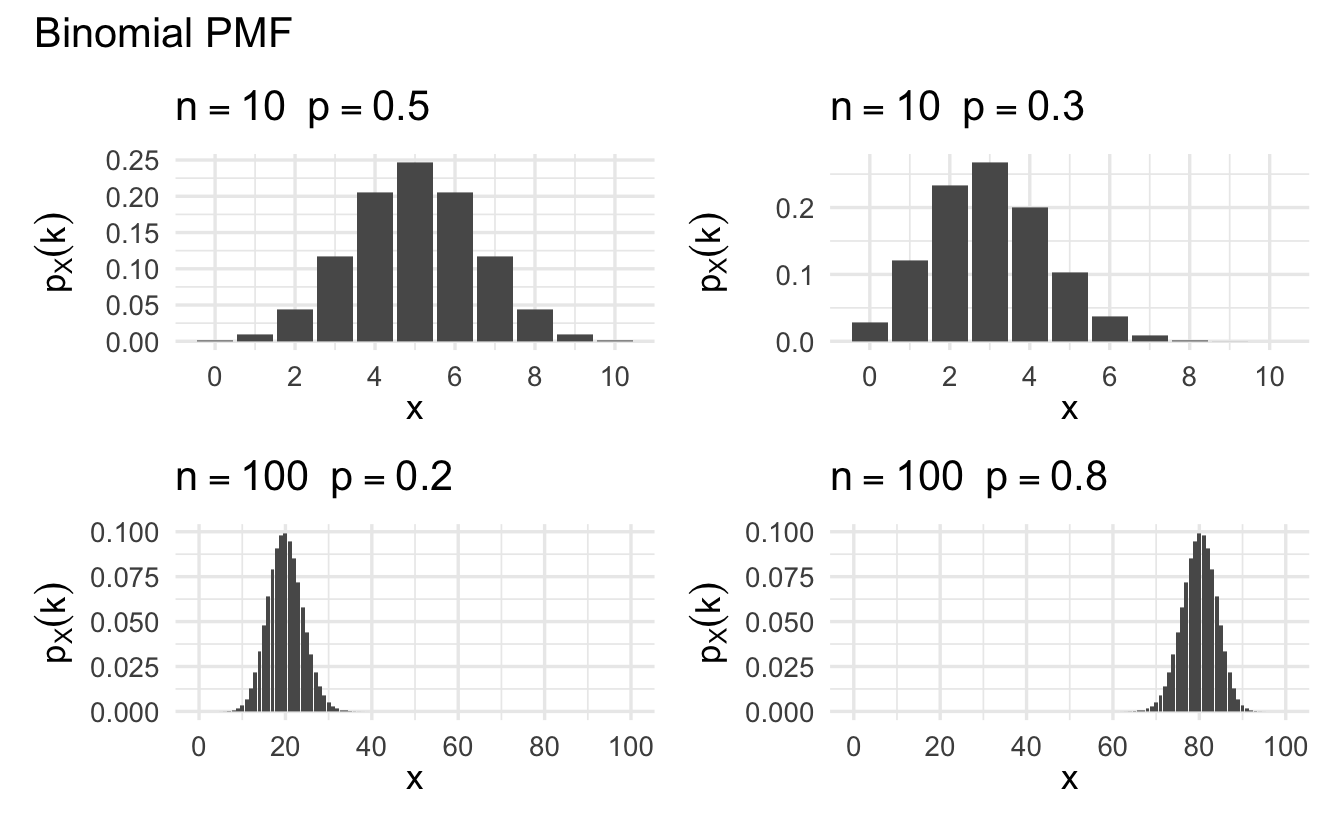
Figure 8.2: Example Binomial probability mass functions
Recall our experiment example:
- \(\Pr(T) = \Pr(C) = 1/2\)
- \(Z =\) number of units assigned to treatment
\[ \begin{aligned} Z & \sim \text{Binomial}(1/2)\\ p_Z(0) & = {{3}\choose{0}} (1/2)^{0} (1- 1/2)^{3-0} = 1 \times \frac{1}{8}\\ p_Z(1) & = {{3}\choose{1}} (1/2)^{1} (1 - 1/2)^{2} = 3 \times \frac{1}{8} \\ p_Z(2) & = {{3}\choose{2}} (1/2)^{2} (1- 1/2)^1 = 3 \times \frac{1}{8} \\ p_Z(3) & = {{3}\choose{3}} (1/2)^{3} (1 - 1/2)^{0} = 1 \times \frac{1}{8} \end{aligned} \]
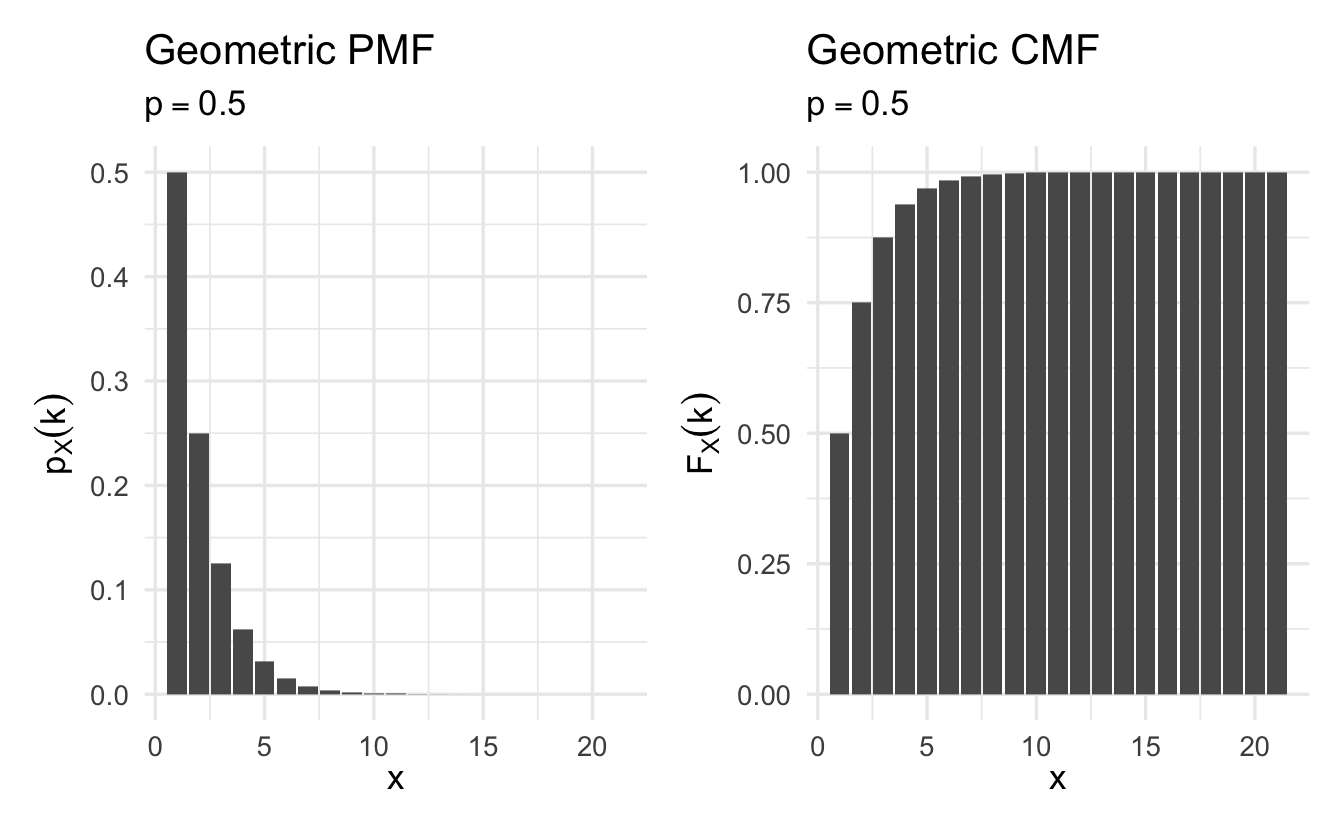
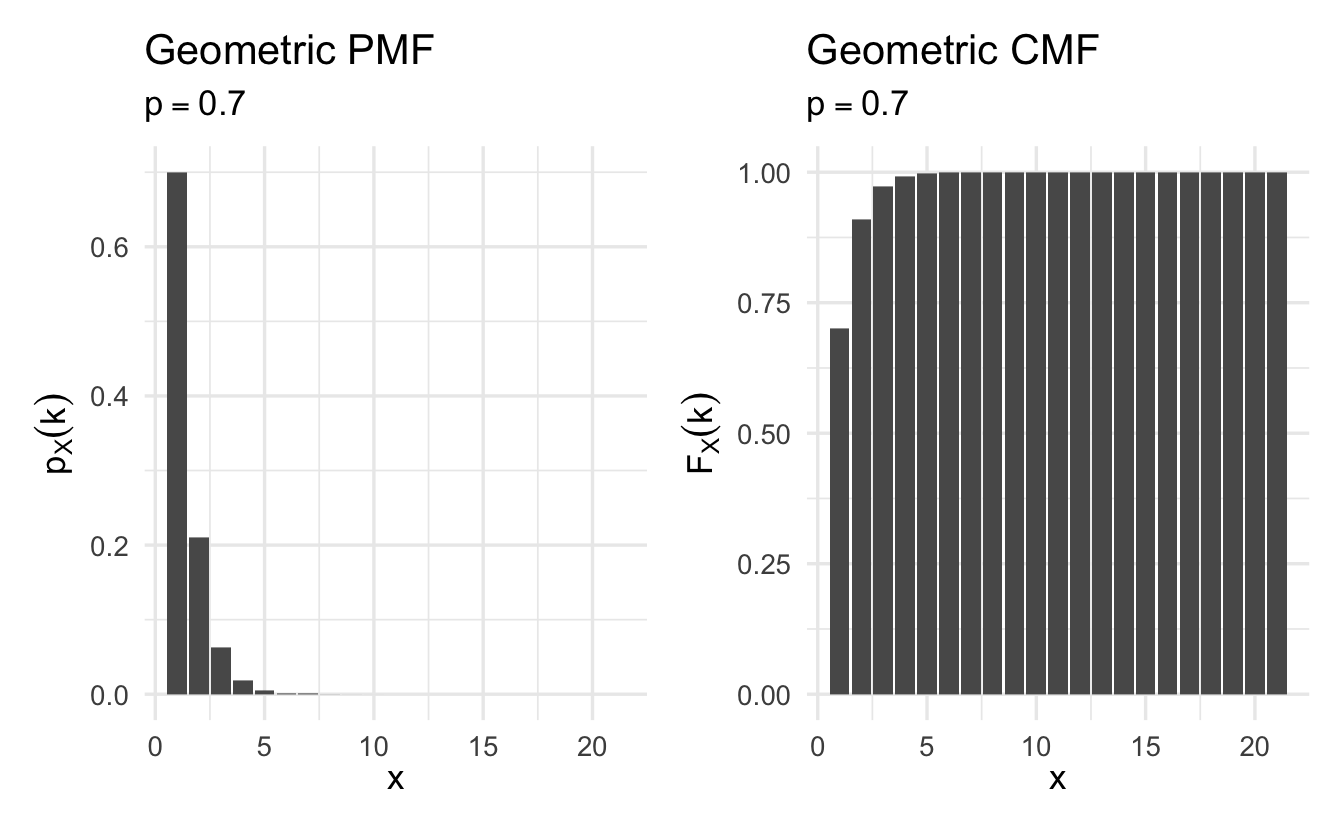
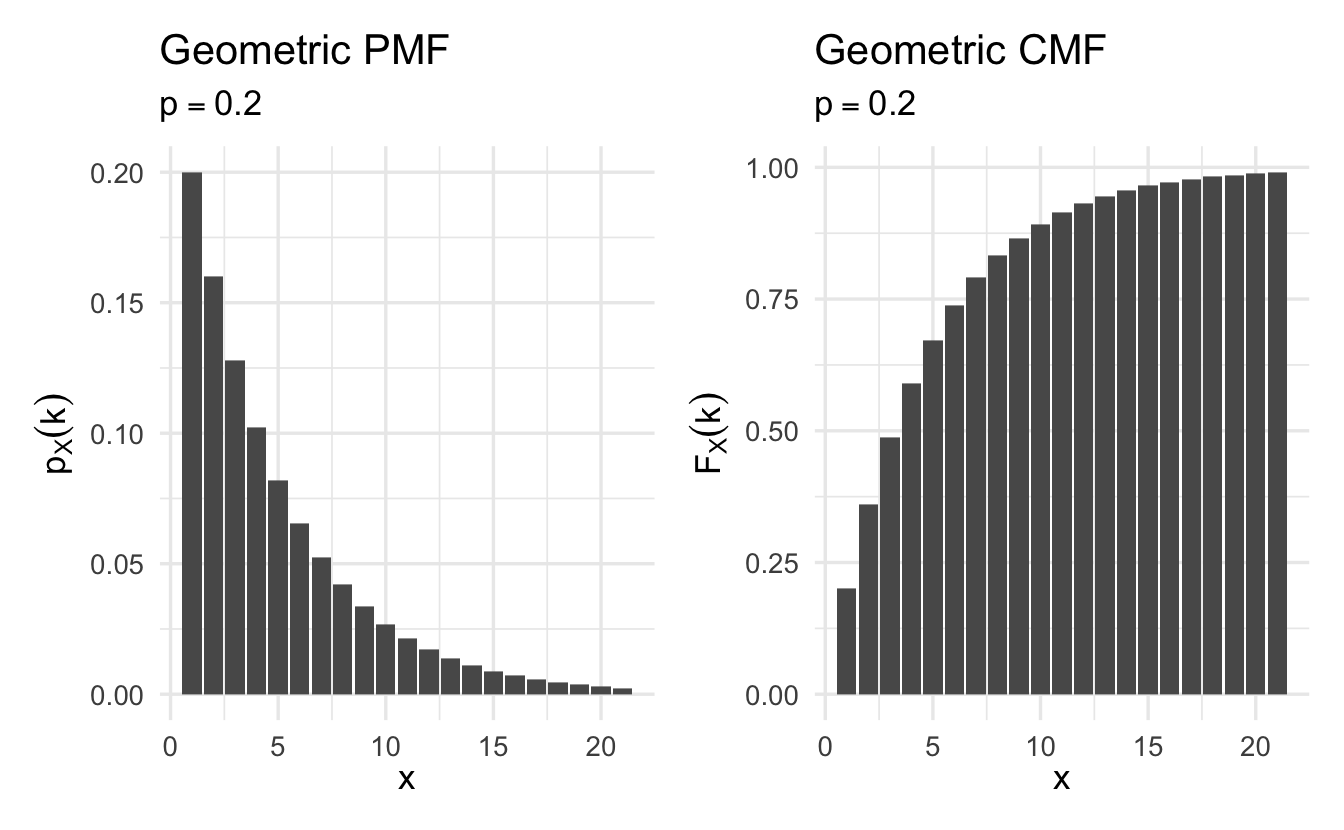
8.4.3 Geometric
- A model to count the number of trials of a Bernoulli outcome before success occurs the first time
Definition 8.5 (Geometric random variable) Suppose \(X\) is a random variable that counts the number of tosses needed for a head to come up the first time. Its PMF is
\[p_X(k) = (1 - p)^{k-1}p, \quad k = 1, 2, \ldots\]
\((1 - p)^{k-1}p\) is the probability of the sequence consisting of \(k-1\) successive trials followed by a head. This is a valid PMF because
\[ \begin{aligned} \sum_{k=1}^{\infty} p_X(k) &= \sum_{k=1}^{\infty} (1 - p)^{k-1}p \\ &= p \sum_{k=1}^{\infty} (1 - p)^{k-1} \\& = p \times \frac{1}{1 - (1-p)} \\ &= 1 \end{aligned} \]
Geometric random variables can be used to count the number of trials of a Bernoulli outcome before success occurs the first time.
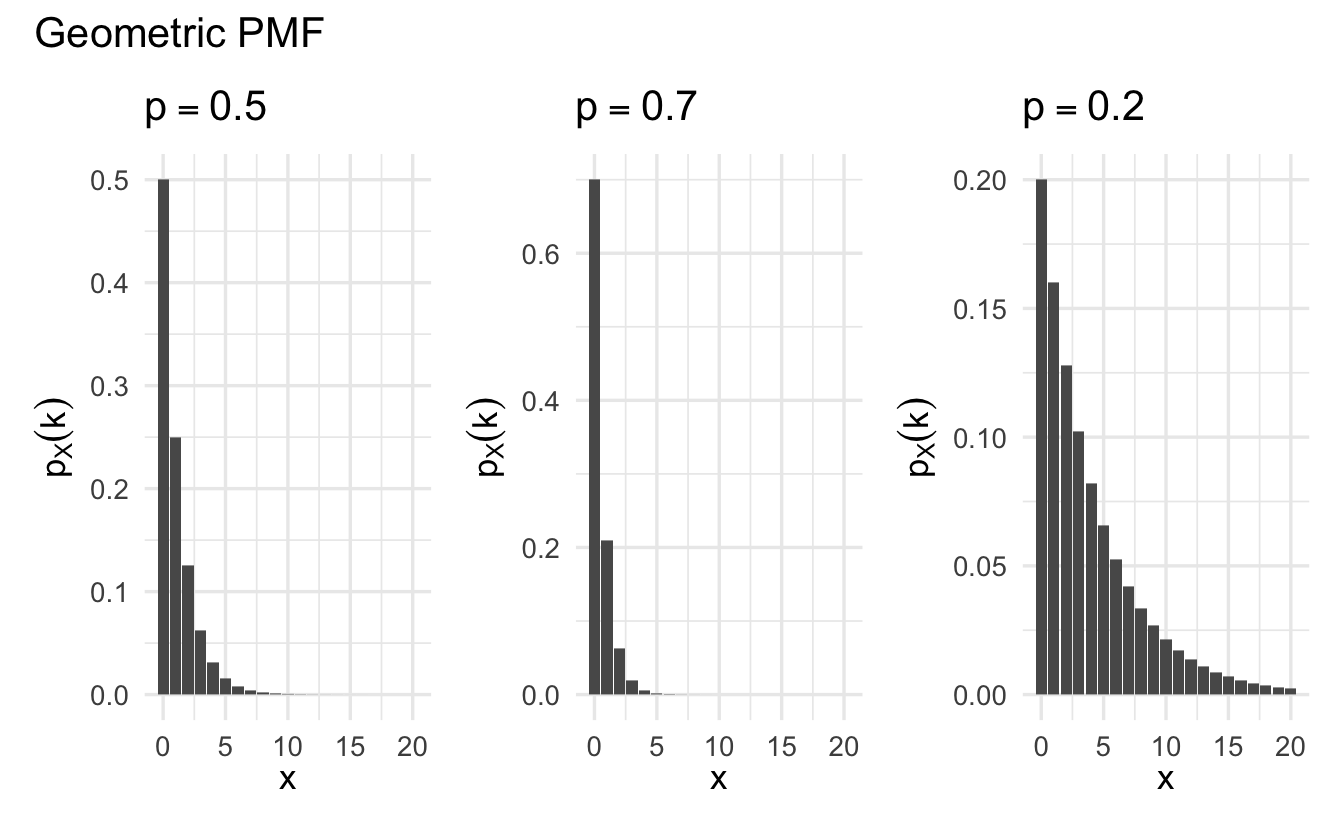
Figure 8.3: Example Geometric probability mass functions
Examples include:
- Number of attempts before passing a test
- Finding a missing item in a search
8.4.4 Poisson
Often social scientists are interested in counting the number of events that occur:
- Number of wars started
- Number of speeches made
- Number of bribes offered
- Number of people waiting for license
These are generally referred to as event counts.
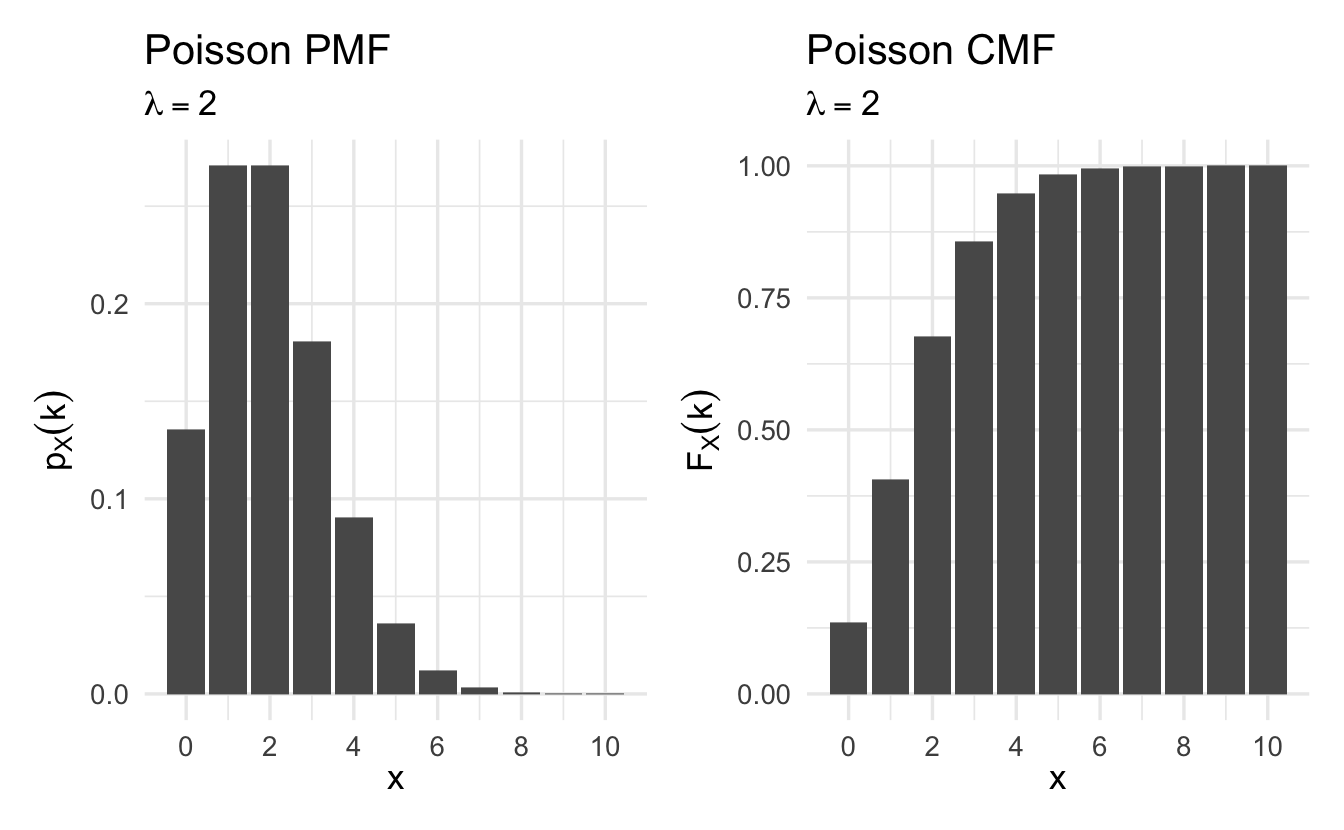
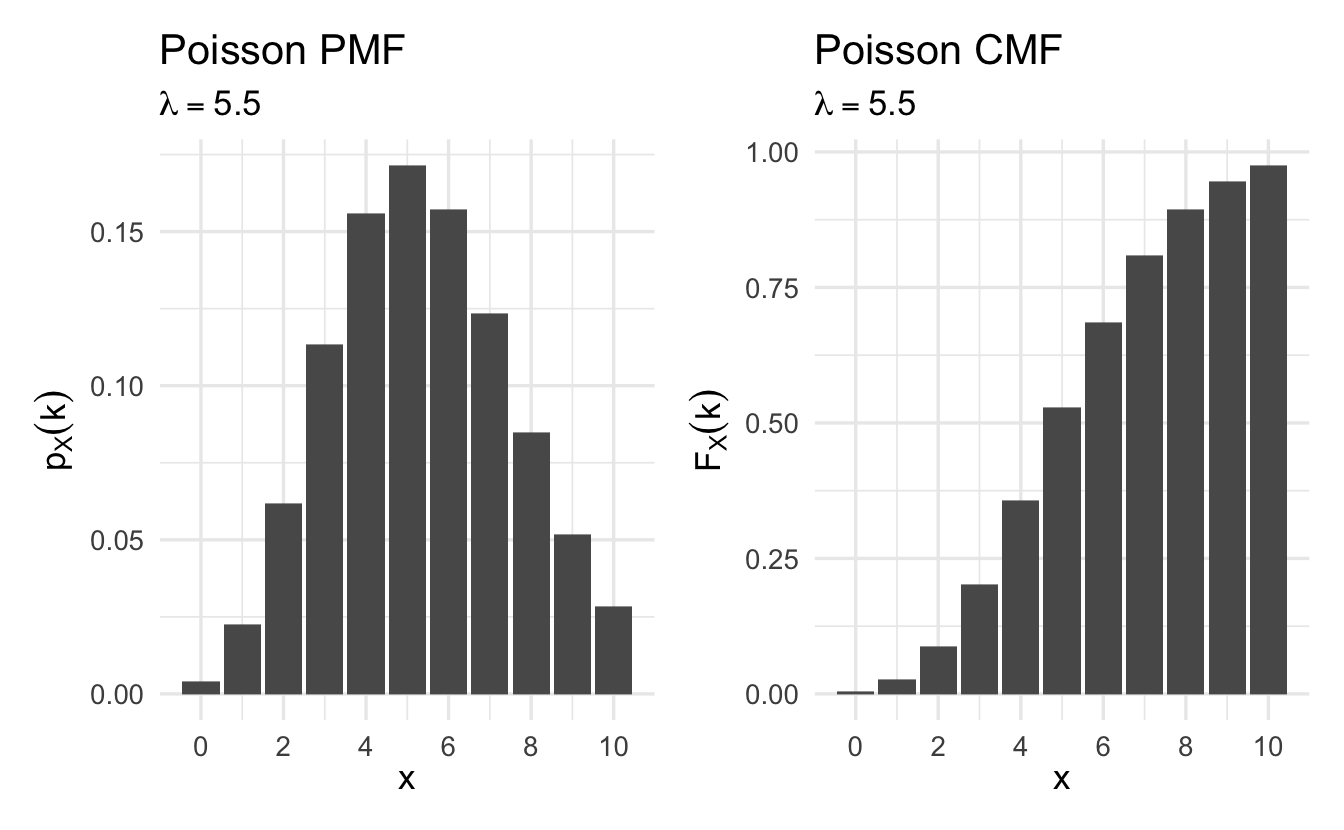
Definition 8.6 (Poisson random variable) Suppose \(X\) is a random variable that takes on values \(X \in \{0, 1, 2, \ldots, \}\) and that \(\Pr(X = k) = p_X(k)\) is,
\[p_X(k) = e^{-\lambda} \frac{\lambda^{k}}{k!}, \quad k = 0,1,2,\ldots\]
for \(k \in \{0, 1, \ldots, \}\) and \(0\) otherwise. Then we will say that \(X\) follows a Poisson distribution with rate parameter \(\lambda\)
\[X \sim \text{Poisson}(\lambda)\]
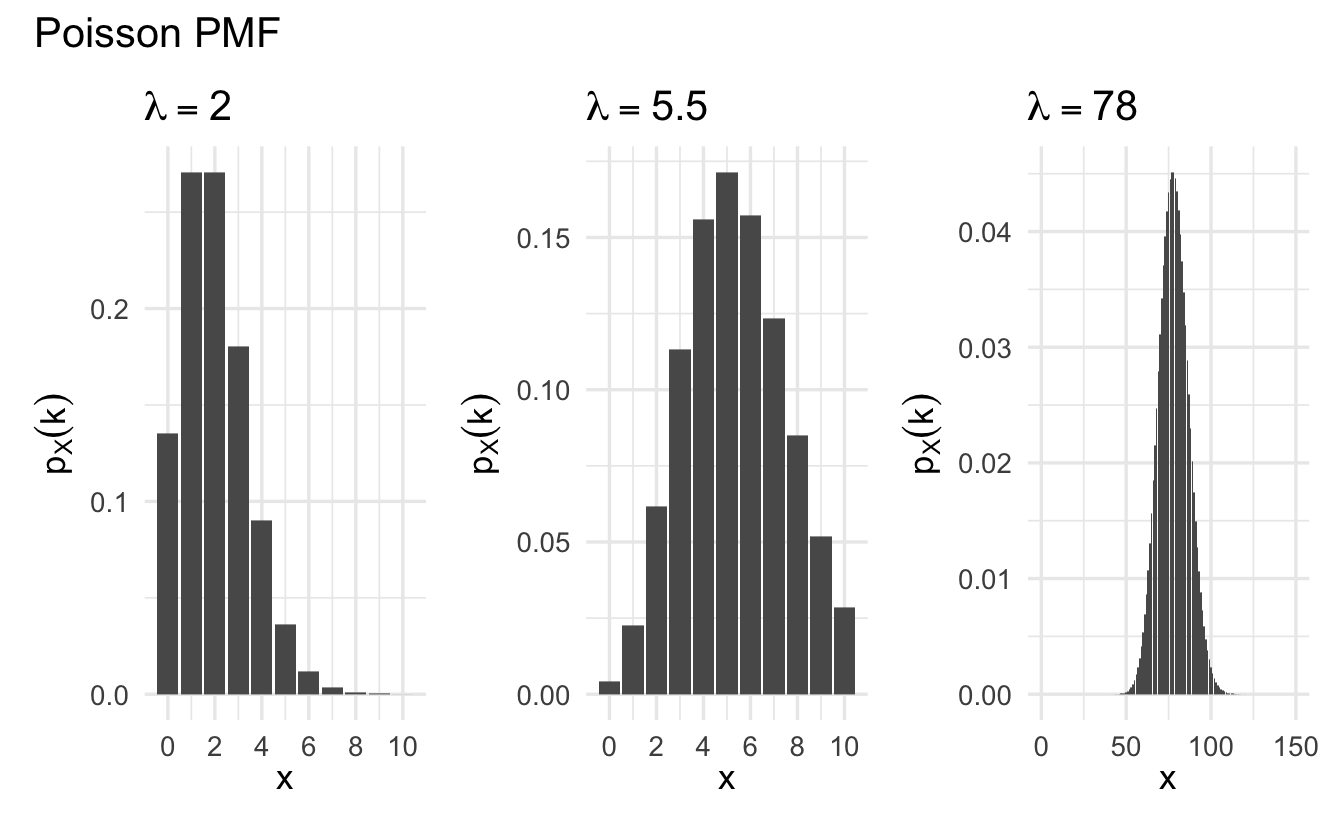
Figure 8.4: Example Poisson probability mass functions
Example 8.6 (Presidential threats) Suppose the number of threats a president makes in a term is given by \(X \sim \text{Poisson}(5)\)18 What is the probability the president will make ten threats?
\[p_X(10) = e^{-\lambda} \frac{5^{10}}{10!}\]
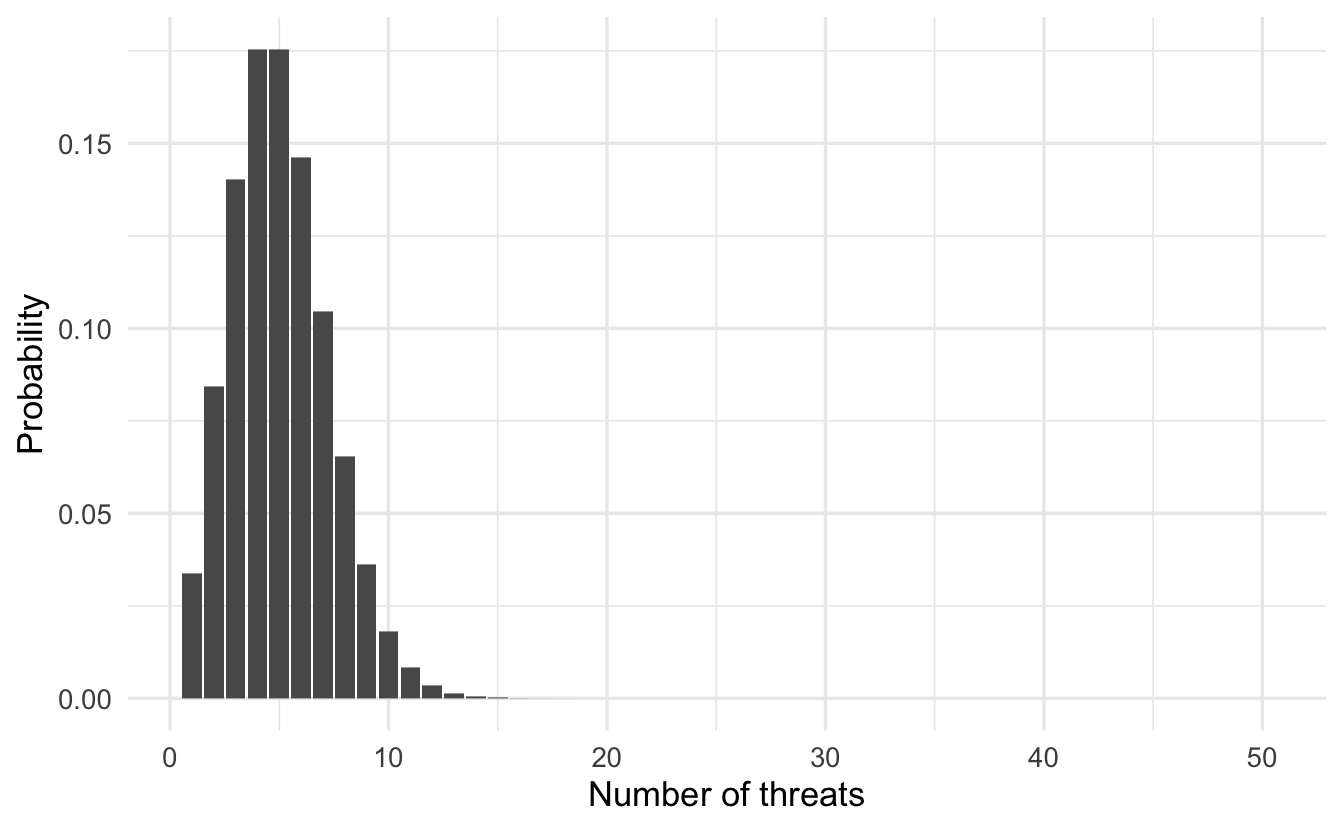
8.4.4.1 Approximating a binomial random variable
The Poisson PMF with parameter \(\lambda\) is a good approximation for a binomial PMF with parameters \(n\) and \(p\)
\[e^{-\lambda} \frac{\lambda^{k}}{k!} \approx {{N}\choose{k}}\pi^{k} (1- \pi)^{n-k}, \quad \text{if } k \ll n\]
provided \(\lambda = np\), \(n\) is very large, and \(p\) is very small. Sometimes using the Poisson PMF results in simpler models and easier calculations. For instance, \(n = 100\) and \(p = 0.01\).
Using the binomial PMF
\[\frac{100!}{95! 5!} \times 0.01^5 (1 - 0.01)^{95} = 0.00290\]
Versus using the Poisson PMF with \(\lambda = np = 100 \times 0.01 = 1\)
\[e^{-1} \frac{1}{5!} = 0.00306\]
8.5 Functions of random variables
Given a random variable \(X\), you may wish to create a new random variable \(Y\) using transformations of \(X\). This could be a linear function of the form
\[Y = g(X) = aX + b\]
where \(a\) and \(b\) are scalars. It could be a logarithmic transformation
\[g(X) = \log(X)\]
If \(Y = g(X)\) is a function of a random variable \(X\), then \(Y\) is also a random variable. All outcomes in the sample space defined with a numerical value \(x\) for \(X\) also have a numerical value \(y = g(x)\) for \(Y\).
8.6 Expectation, mean, and variance
The PMF of a random variable \(X\) provides several numbers – the probabilities of all possible values of \(X\). Often it is desirable to summarize this information into a single representative number: the expectation of \(X\) – weighted average of the possible values of \(X\).
8.6.1 Motivation
Consider spinning a wheel of fortune many times. At each spin, one of the numbers \(m_1, m_2, \ldots, m_n\) comes up with corresponding probability \(p_1, p_2, \ldots, p_n\), and this is your monetary reward from that spin. What is the amount of money that you “expect” to get “per spin”? The terms “expect” and “per spin” are a little ambiguous, but here is a reasonable interpretation.
Suppose you spin the wheel \(k\) times, and that \(k_i\) is the number of times that the outcome is \(m_i\). Then, the total amount received is \(m_1 k_1 + m_2 k_2 + \ldots + m_n k_n\). The amount received per spin is a simple average:
\[M = \frac{m_1 k_1 + m_2 k_2 + \ldots + m_n k_n}{k}\]
If the number of spins \(k\) is very large and we interpret probabilities as relative frequencies, we could anticipate that \(m_i\) comes up a fraction of times roughly equal to \(p_i\):
\[\frac{k_i}{k} \approx p_i, i = 1, \ldots,n\]
Thus, the amount of money you “expect” to receive is
\[M = \frac{m_1 k_1 + m_2 k_2 + \ldots + m_n k_n}{k} \approx m_1p_1 + m_2p_2 + \ldots + m_np_n\]
8.6.2 Expectation
Definition 8.7 (Expected value) Define expected value (known as expectation or the mean) of a random variable \(X\), with PMF \(p_X\) as
\[\E[X] = \sum_{x:p(x)>0} x p(x)\]
where \(\sum_{x:p(x)>0}\) is all values of \(X\) with probability greater than 0.
In words: for all values of \(x\) with \(p(x)\) greater than zero, take the weighted average of the values.
Example 8.7 Suppose \(X\) is number of units assigned to treatment, in one of our previous example.
\[ X = \left \{ \begin{array} {ll} 0 \text{ if } (C, C, C) \\ 1 \text{ if } (T, C, C) \text{ or } (C, T, C) \text{ or } (C, C, T) \\ 2 \text{ if } (T, T, C) \text{ or } (T, C, T) \text{ or } (C, T, T) \\ 3 \text{ if } (T, T, T) \end{array} \right. \]
What is \(\E[X]\)?
\[ \begin{aligned} \E[X] & = 0\times \frac{1}{8} + 1 \times \frac{3}{8} + 2 \times \frac{3}{8} + 3 \times \frac{1}{8} \\ & = 1.5 \end{aligned} \]
The expected value is essentially a weighted average, or the average outcome (value in the middle of the range). It gives us a measure of central tendency.
Example 8.8 (A single person poll) Suppose that there is a group of \(N\) people. Suppose \(M< N\) people approve of Donald Trump’s performance as president, and \(N - M\) disapprove of his performance.
Draw one person \(i\), with \(\Pr(\text{Draw } i ) = \frac{1}{N}\)
\[ X = \left \{ \begin{array} {ll} 1 \text{ if person Approves} \\ 0 \text{ if Disapproves} \\ \end{array} \right. \]
What is \(\E[X]\)?
\[ \begin{aligned} \E[X] & = 1 \times \Pr(\text{Approve}) + 0 \times \Pr(\text{Disapprove}) \\ & = 1 \times \frac{M}{N} \\ & = \frac{M}{N} \end{aligned} \]
8.6.2.1 Indicator variables and probabilities
Proposition 8.1 Suppose \(A\) is an event. Define random variable \(I\) such that \(I= 1\) if an outcome in \(A\) occurs and \(I =0\) if an outcome in \(A^{c}\) occurs. Then,
\[\E[I] = \Pr(A)\]
Proof. \[ \begin{aligned} \E[I] & = 1 \times \Pr(A) + 0 \times \Pr(A^{c}) \\ & = \Pr(A) \end{aligned} \]
8.6.3 Variance, moments, and the expected value rule
Other quantities we care about include variance and moments.
8.6.3.1 Moments
- 1st moment: \(\E[X^1] = \E[X]\) - that is, the mean
- 2nd moment: \(\E[X^2]\)
- \(n\)th moment: \(\E[X^n]\)
8.6.3.2 Variance
Expected value is a measure of central tendency. What about spread or dispersion?
For each value, we might measure distance from the center. For example, Euclidean distance is squared \(d(x, E[X])^{2} = (x - E[X])^2\)
Then, we might take weighted average of these distances
\[ \begin{aligned} \E[(X - \E[X])^2] & = \sum_{x:p_X(x)>0} (x - \E[X])^2p_X(x) \\ & = \sum_{x:p_X(x)>0} \left(x^2 p_X(x)\right) - 2 \E[X]\sum_{x:p_X(x)>0} \left(x p_X(x)\right) + \E[X]^2\sum_{x:p_X(x)>0} p_X(x) \\ & = \E[X^2] - 2\E[X]^2 + \E[X]^2 \\ & = \E[X^2] - \E[X]^2 \\ & = \text{Var}(X) \end{aligned} \]
Defined as the expected value of the random variable \((X - \E[X])^2\)
\[ \begin{aligned} \Var(X) &= \E[(X - \E[X])^2] \\ &= \E[X^2] - \E[X]^2 \end{aligned} \]
- Since \((X - \E[X])^2\) can only take non-negative values, \(\Var(X) \geq 0\)
This is a measure of dispersion of \(X\) around its mean. We will define the standard deviation of \(X\), \(\sigma_X = \sqrt{\Var(X)}\). Standard deviation is easier to interpret sometimes since it is in the same units as \(X\).
8.6.3.2.1 Calculating variance of a random variable
We could generate the PMF of the random variable \((X - \E[X])^2\), then calculate the expectation of this function – it is just a linear function.
Instead, we can take a shortcut: the expected value rule for functions of random variables. Let \(X\) be a random variable with PMF \(p_X\), and let \(g(X)\) be a function of \(X\). Then, the expected value of the random variable \(g(X)\) is given by
\[\E[g(X)] = \sum_{x} g(x) p_X(x)\]
This allows us to rewrite our variance formula:
\[ \begin{align} \Var(X) &= \E[(X - \E[X])^2] \\ \Var(X) &= \E[X^2] - \E[X]^2 \end{align} \]
We just need the first and second moments to calculate variance.
8.6.4 Practice calculating expectation and variance
8.6.4.1 Bernoulli variable
Suppose \(Y \sim \text{Bernoulli}(\pi)\)
\[ \begin{aligned} \E[Y] & = 1 \times \Pr(Y = 1) + 0 \times \Pr(Y = 0) \nonumber \\ & = \pi + 0 (1 - \pi) \nonumber = \pi \\ \Var(Y) & = \E[Y^2] - \E[Y]^2 \nonumber \\ \E[Y^2] & = 1^{2} \Pr(Y = 1) + 0^{2} \Pr(Y = 0) \nonumber \\ & = \pi \nonumber \\ \Var(Y) & = \pi - \pi^{2} \nonumber \\ & = \pi(1 - \pi ) \nonumber \end{aligned} \]
\(\E[Y] = \pi\)
\(\Var(Y) = \pi(1- \pi)\)
What is the maximum variance?
\[ \begin{aligned} \Var(Y) & = \pi - \pi^{2} \nonumber \\ & = 0.5(1 - 0.5 ) \\ & = 0.25 \end{aligned} \]
8.6.5 Decision making using expected values
We can use expected values to optimizes the choice between several candidate decisions that result in random rewards. View the expected reward of a decision as its average payoff over a large number of trials, and choose a decision with maximum expected reward.
Example 8.9 (Going to war) Suppose country \(1\) is engaged in a conflict and can either win or lose. Define \(Y = 1\) if the country wins and \(Y = 0\) otherwise. Then,
\[Y \sim \text{Bernoulli}(\pi)\]
Suppose country \(1\) is deciding whether to fight a war. Engaging in the war will cost the country \(c\). If they win, country \(1\) receives \(B\). What is \(1\)’s expected utility from fighting a war?
\[ \begin{aligned} \E[U(\text{war})] & = U(\text{war} | \text{win}) \times \Pr(\text{win}) + U(\text{war} | \text{lose}) \times \Pr(\text{lose}) \\ & = (B - c) \Pr(Y = 1) + (- c) \Pr(Y = 0 ) \\ & = B \times \Pr(Y = 1) - c(\Pr(Y = 1) + \Pr(Y = 0)) \\ & = B \times \pi - c \end{aligned} \]
Based on your beliefs about the appropriate values for \(B, \pi, c\), you can decide whether to engage in the war
- If expected utility is greater than 0, you should decide to go to war
- If expected utility is less than 0, you should decide not to go to war
8.7 Cumulative mass function, redux
The cumulative mass function (CMF) defines the the cumulative probability \(F_X(x)\) up to the value of \(x\). For a discrete random variable \(X\), we define the CMF \(F_X\) which provides the probability \(\Pr (X \leq x)\). For every \(x\)
\[F_X(x) = \Pr (X \leq x) = \sum_{k \leq x} p_X(k)\]
Any random variable associated with a given probability model has a CMF. Basic properties of CMFs for discrete random variables are:
\(F_X\) is monotonically non-decreasing – if \(x \leq y\), then \(F_X(x) \leq F_X(y)\)
\(F_X(x)\) tends to \(0\) as \(x \rightarrow -\infty\), and to \(1\) as \(x \rightarrow \infty\)
\(F_X(x)\) is a piecewise constant function of \(x\)
If \(X\) is discrete and takes integer values, the PMF and the CMF can be obtained from each other by summing or differencing:
\[F_X(k) = \sum_{i = -\infty}^k p_X(i),\] \[p_X(k) = \Pr (X \leq k) - \Pr (X \leq k-1) = F_X(k) - F_X(k-1)\]
for all integers \(k\)
References
Clearly estimated pre-Trump.↩︎