Lecture 5 Functions of several variables and optimization with several variables
Learning objectives
- Define a partial derivative
- Identify higher order derivatives and partial derivatives
- Define notation for calculus performed on vector and matrix forms
- Demonstrate multivariable calculus methods on social scientific research
- Calculate critical points, partial derivatives, and double integrals
Supplemental readings
- Chapter 14, Pemberton and Rau (2011)
- OpenStax Calculus: Volume 3, ch 4
5.1 Higher order derivatives
The first derivative is applying the definition of derivatives on the function, and it can be expressed as
\[f'(x), ~~ y', ~~ \frac{d}{dx}f(x), ~~ \frac{dy}{dx}\]
We can keep applying the differentiation process to functions that are themselves derivatives. The derivative of \(f'(x)\) with respect to \(x\), would then be \[f''(x)=\lim\limits_{h\to 0}\frac{f'(x+h)-f'(x)}{h}\] and we can therefore call it the Second derivative:
\[f''(x), ~~ y'', ~~ \frac{d^2}{dx^2}f(x), ~~ \frac{d^2y}{dx^2}\]
Similarly, the derivative of \(f''(x)\) would be called the third derivative and is denoted \(f'''(x)\). And by extension, the nth derivative is expressed as \(\frac{d^n}{dx^n}f(x)\), \(\frac{d^ny}{dx^n}\).
\[ \begin{aligned} f(x) &=x^3\\ f^{\prime}(x) &=3x^2\\ f^{\prime\prime}(x) &=6x \\ f^{\prime\prime\prime}(x) &=6\\ f^{\prime\prime\prime\prime}(x) &=0\\ \end{aligned} \]
Earlier, we said that if a function is differentiable at a given point, then it must be continuous. Further, if \(f'(x)\) is itself continuous, then \(f(x)\) is called continuously differentiable. All of this matters because many of our findings about optimization rely on differentiation, and so we want our function to be differentiable in as many layers. A function that is continuously differentiable infinitely is called smooth. Some examples include:
\[ \begin{aligned} f(x) &= x^2 \\ f(x) &= e^x \end{aligned} \]
5.2 Multivariate function
A multivariate function is a function with more than one argument.
5.2.0.0.6 Example 6
\[ \begin{aligned} f(\mathbf{x} )&= f(x_{1}, x_{2}, \ldots, x_{N} ) \\ &= x_{1} +x_{2} + \ldots + x_{N} \\ &= \sum_{i=1}^{N} x_{i} \end{aligned} \]
5.2.1 Definition
Definition 5.1 (Multivariate function) Suppose \(f:\Re^{n} \rightarrow \Re^{1}\). We will call \(f\) a multivariate function. We will commonly write,
\[f(\mathbf{x}) = f(x_{1}, x_{2}, x_{3}, \ldots, x_{n} )\]
- \(\Re^{n} = \Re \underbrace{\times}_{\text{cartesian}} \Re \times \Re \times \ldots \Re\)
- The function we consider will take \(n\) inputs and output a single number (that lives in \(\Re^{1}\), or the real line)
5.2.2 Evaluating multivariate functions
Example 5.1 \[f(x_{1}, x_{2}, x_{3}) = x_1 + x_2 + x_3\]
Evaluate at \(\mathbf{x} = (x_{1}, x_{2}, x_{3}) = (2, 3, 2)\)
\[ \begin{aligned} f(2, 3, 2) & = 2 + 3 + 2 \\ & = 7 \end{aligned} \]
Example 5.2 \[f(x_{1}, x_{2} ) = x_{1} + x_{2} + x_{1} x_{2}\]
Evaluate at \(\mathbf{w} = (w_{1}, w_{2} ) = (1, 2)\)
\[ \begin{aligned} f(w_{1}, w_{2}) & = w_{1} + w_{2} + w_{1} w_{2} \\ & = 1 + 2 + 1 \times 2 \\ & = 5 \end{aligned} \]
Example 5.3 (Preferences for multidimensional policy) Recall that in the spatial model, we suppose policy and political actors are located in a space. Suppose that policy is \(N\) dimensional - or \(\mathbf{x} \in \Re^{N}\). Suppose that legislator \(i\)’s utility is a \(U:\Re^{N} \rightarrow \Re^{1}\) and is given by,
\[ \begin{aligned} U(\mathbf{x}) & = U(x_{1}, x_{2}, \ldots, x_{N} ) \\ & = - (x_{1} - \mu_{1} )^2 - (x_{2} - \mu_{2})^2 - \ldots - (x_{N} - \mu_{N})^{2} \\ & = -\sum_{j=1}^{N} (x_{j} - \mu_{j} )^{2} \end{aligned} \]
Suppose \(\mathbf{\mu} = (\mu_{1}, \mu_{2}, \ldots, \mu_{N} ) = (0, 0, \ldots, 0)\). Evaluate legislator’s utility for a policy proposal of \(\mathbf{m} = (1, 1, \ldots, 1)\)
\[ \begin{aligned} U(\mathbf{m} ) & = U(1, 1, \ldots, 1) \\ & = - (1 - 0)^2 - (1- 0) ^2 - \ldots - (1- 0) ^2 \\ & = -\sum_{j=1}^{N} 1 = - N \\ \end{aligned} \]
Example 5.4 (Regression models and randomized treatments) Often we administer randomized experiments. The most recent wave of interest began with voter mobilization, and wonders if individual \(i\) turns out to vote, \(\text{Vote}_{i}\)
- \(T = 1\) (treated): voter receives mobilization
- \(T = 0\) (control): voter does not receive mobilization
Suppose we find the following regression model, where \(x_{2}\) is a participant’s age:
\[ \begin{aligned} f(T,x_2) & = \Pr(\text{Vote}_{i} = 1 | T, x_{2} ) \\ & = \beta_{0} + \beta_{1} T + \beta_{2} x_{2} \end{aligned} \]
We can calculate the effect of the experiment as:
\[ \begin{aligned} f(T = 1, x_2) - f(T=0, x_2) & = \beta_{0} + \beta_{1} 1 + \beta_{2} x_{2} - (\beta_{0} + \beta_{1} 0 + \beta_{2} x_{2}) \\ & = \beta_{0} - \beta_{0} + \beta_{1}(1 - 0) + \beta_{2}(x_{2} - x_{2} ) \\ & = \beta_{1} \end{aligned} \]
5.3 Multivariate derivatives
What happens when there’s more than one variable that is changing?
Suppose we have a function \(f\) now of two (or more) variables and we want to determine the rate of change relative to one of the variables. To do so, we would find its partial derivative, which is defined similar to the derivative of a function of one variable.
Definition 5.2 (Partial derivative) Let \(f\) be a function of the variables \((x_1,\ldots,x_n)\). The partial derivative of \(f\) with respect to \(x_i\) is
\[\frac{\partial f}{\partial x_i} (x_1,\ldots,x_n) = \lim\limits_{h\to 0} \frac{f(x_1,\ldots,x_i+h,\ldots,x_n)-f(x_1,\ldots,x_i,\ldots,x_n)}{h}\]
Only the \(i\)th variable changes — the others are treated as constants.
We can take higher-order partial derivatives, like we did with functions of a single variable, except now the higher-order partials can be with respect to multiple variables.
Notice that you can take partials with regard to different variables.
Suppose \(f(x,y)=x^2+y^2\). Then
\[ \begin{aligned} \frac{\partial f}{\partial x}(x,y) &= 2x \\ \frac{\partial f}{\partial y}(x,y) &= 2y\\ \frac{\partial^2 f}{\partial x^2}(x,y) &= 2\\ \frac{\partial^2 f}{\partial x \partial y}(x,y) &= 0 \end{aligned} \]
Let \(f(x,y)=x^3 y^4 +e^x -\log y\). What are the following partial derivaitves?
\[ \begin{aligned} \frac{\partial f}{\partial x}(x,y) &= 3x^2y^4 + e^x\\ \frac{\partial f}{\partial y}(x,y) &=4x^3y^3 - \frac{1}{y}\\ \frac{\partial^2 f}{\partial x^2}(x,y) &= 6xy^4 + e^x\\ \frac{\partial^2 f}{\partial x \partial y}(x,y) &= 12x^2y^3 \end{aligned} \]
Example 5.5 (Rate of change, linear regression) Suppose we regress \(\text{Approval}_{i}\) rate for Trump in month \(i\) on \(\text{Employ}_{i}\) and \(\text{Gas}_{i}\). We obtain the following model:
\[\text{Approval}_{i} = 0.8 -0.5 \text{Employ}_{i} -0.25 \text{Gas}_{i}\]
We are modeling \(\text{Approval}_{i} = f(\text{Employ}_{i}, \text{Gas}_{i} )\). What is the partial derivative with respect to employment?
\[\frac{\partial f(\text{Employ}_{i}, \text{Gas}_{i} ) }{\partial \text{Employ}_{i} } = -0.5\]
5.4 Multivariate optimization
Just as we want to optimize functions with a single variable, we often wish to opimize functions with multiple variables.
Parameters \(\mathbf{\beta} = (\beta_{1}, \beta_{2}, \ldots, \beta_{n} )\) such that \(f(\mathbf{\beta}| \mathbf{X}, \mathbf{Y})\) is maximized
Policy \(\mathbf{x} \in \Re^{n}\) that maximizes \(U(\mathbf{x})\)
Weights \(\mathbf{\pi} = (\pi_{1}, \pi_{2}, \ldots, \pi_{K})\) such that a weighted average of forecasts \(\mathbf{f} = (f_{1} , f_{2}, \ldots, f_{k})\) have minimum loss
\[\min_{\mathbf{\pi}} = - (\sum_{j=1}^{K} \pi_{j} f_{j} - y ) ^ 2\]
As before, we will consider both analytic and computational approaches.
5.4.1 Differences from single variable optimization procedure
It is the same basic approach, except we have multiple parameters of interest. This requires more explicit knowledge of linear algebra to track all the components and optimize over the multidimensional space
Let \(\mathbf{x} \in \Re^{n}\) and let \(\delta >0\). Define a neighborhood of \(\mathbf{x}\), \(B(\mathbf{x}, \delta)\), as the set of points such that,
\[B(\mathbf{x}, \delta) = \{ \mathbf{y} \in \Re^{n} : ||\mathbf{x} - \mathbf{y}||< \delta \}\]
- That is, \(B(\mathbf{x}, \delta)\) is the set of points where the vector \(\mathbf{y}\) is a vector in n-dimensional space such that vector norm of \(\mathbf{x} - \mathbf{y}\) is less than \(\delta\)
- So the neighborhood is at most \(\delta\) big
Now suppose \(f:X \rightarrow \Re\) with \(X \subset \Re^{n}\). A vector \(\mathbf{x}^{*} \in X\) is a global maximum if , for all other \(\mathbf{x} \in X\)
\[f(\mathbf{x}^{*}) > f(\mathbf{x} )\]
A vector \(\mathbf{x}^{\text{local}}\) is a local maximum if there is a neighborhood around \(\mathbf{x}^{\text{local}}\), \(Q \subset X\) such that, for all \(x \in Q\),
\[f(\mathbf{x}^{\text{local} }) > f(\mathbf{x} )\]
The maximum and minimum values of a function \(f:X \rightarrow \Re\) on the real number line (in n-dimensional space) will fall somewhere along \(X\). This is the same as we saw previously, except now \(X\) is not a scalar value - it is a vector \(\mathbf{X}\).
5.4.2 First derivative test: Gradient
Suppose \(f:X \rightarrow \Re^{n}\) with \(X \subset \Re^{1}\) is a differentiable function. Define the gradient vector of \(f\) at \(\mathbf{x}_{0}\), \(\nabla f(\mathbf{x}_{0})\) as
\[\nabla f (\mathbf{x}_{0}) = \left(\frac{\partial f (\mathbf{x}_{0}) }{\partial x_{1} }, \frac{\partial f (\mathbf{x}_{0}) }{\partial x_{2} }, \frac{\partial f (\mathbf{x}_{0}) }{\partial x_{3} }, \ldots, \frac{\partial f (\mathbf{x}_{0}) }{\partial x_{n} } \right)\]
- It is the first partial derivatives for each variable \(x_n\) stored in a vector
- Gradient points in the direction that the function is increasing in the fastest direction
So if \(\mathbf{a} \in X\) is a local extremum, then,
\[ \begin{aligned} \nabla f(\mathbf{a}) &= \mathbf{0} \\ &= (0, 0, \ldots, 0) \end{aligned} \]
That is, the root(s) of the gradient are where \(f(\mathbf{a})\) equals \(\mathbf{0}\) in \(n\)-dimensional space.
Example 5.6 \[ \begin{aligned} f(x,y) &= x^2+y^2 \\ \nabla f(x,y) &= (2x, \, 2y) \end{aligned} \]
Example 5.7 \[ \begin{aligned} f(x,y) &= x^3 y^4 +e^x -\log y \\ \nabla f(x,y) &= (3x^2 y^4 + e^x, \, 4x^3y^3 - \frac{1}{y}) \end{aligned} \]
5.4.3 Second derivative test: Hessian
Suppose \(f:X \rightarrow \Re^{1}\) , \(X \subset \Re^{n}\), with \(f\) a twice differentiable function. We will define the Hessian matrix as the matrix of second derivatives at \(\mathbf{x}^{*} \in X\),
\[ \mathbf{H}(f)(\mathbf{x}^{*} ) = \begin{bmatrix} \frac{\partial^{2} f }{\partial x_{1} \partial x_{1} } (\mathbf{x}^{*} ) & \frac{\partial^{2} f }{\partial x_{1} \partial x_{2} } (\mathbf{x}^{*} ) & \ldots & \frac{\partial^{2} f }{\partial x_{1} \partial x_{n} } (\mathbf{x}^{*} ) \\ \frac{\partial^{2} f }{\partial x_{2} \partial x_{1} } (\mathbf{x}^{*} ) & \frac{\partial^{2} f }{\partial x_{2} \partial x_{2} } (\mathbf{x}^{*} ) & \ldots & \frac{\partial^{2} f }{\partial x_{2} \partial x_{n} } (\mathbf{x}^{*} ) \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f }{\partial x_{n} \partial x_{1} } (\mathbf{x}^{*} ) & \frac{\partial^{2} f }{\partial x_{n} \partial x_{2} } (\mathbf{x}^{*} ) & \ldots & \frac{\partial^{2} f }{\partial x_{n} \partial x_{n} } (\mathbf{x}^{*} ) \\ \end{bmatrix} \]
Hessians are symmetric, and they describe the curvature of the function (think, how bended). To calculate the hessian, you must differentiate on the entire gradient with respect to each \(x_n\).
Example 5.8 \[ \begin{aligned} f(x,y) &= x^2+y^2 \\ \nabla f(x,y) &= (2x, \, 2y) \\ \mathbf{H}(f)(x,y) &= \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \end{aligned} \]
Example 5.9 \[ \begin{aligned} f(x,y) &= x^3 y^4 +e^x -\log y \\ \nabla f(x,y) &= (3x^2 y^4 + e^x, \, 4x^3y^3 - \frac{1}{y}) \\ \mathbf{H}(f)(x,y) &= \begin{bmatrix} 6xy^4 + e^x & 12x^2y^3 \\ 12x^2y^3 & 12x^3y^2 + \frac{1}{y^2} \end{bmatrix} \end{aligned} \]
5.4.3.1 Definiteness of a matrix
Consider \(n \times n\) matrix \(\mathbf{A}\). If, for all \(\mathbf{x} \in \Re^{n}\) where \(\mathbf{x} \neq \mathbf{0}\):
\[ \begin{aligned} \mathbf{x}^{'} \mathbf{A} \mathbf{x} &> 0, \quad \mathbf{A} \text{ is positive definite} \\ \mathbf{x}^{'} \mathbf{A} \mathbf{x} &< 0, \quad \mathbf{A} \text{ is negative definite } \end{aligned} \]
If \(\mathbf{x}^{'} \mathbf{A} \mathbf{x} >0\) for some \(\mathbf{x}\) and \(\mathbf{x}^{'} \mathbf{A} \mathbf{x}<0\) for other \(\mathbf{x}\), then we say \(\mathbf{A}\) is indefinite.
5.4.3.2 Second derivative test
- If \(\mathbf{H}(f)(\mathbf{a})\) is positive definite then \(\mathbf{a}\) is a local minimum
- If \(\mathbf{H}(f)(\mathbf{a})\) is negative definite then \(\mathbf{a}\) is a local maximum
- If \(\mathbf{H}(f)(\mathbf{a})\) is indefinite then \(\mathbf{a}\) is a saddle point
5.4.3.3 Use the determinant to assess definiteness
How do we measure definiteness when up until now \(\mathbf{x}\) could be any vector? We can use the determinant of the Hessian of \(f\) at the critical value \(\mathbf{a}\):
\[ \mathbf{H}(f)(\mathbf{a}) = \begin{bmatrix} A & B \\ B & C \\ \end{bmatrix} \]
The determinant for a \(2 \times 2\) matrix can easily be calculated using the known formula \(AC - B^2\).
- \(AC - B^2> 0\) and \(A>0\) \(\leadsto\) positive definite \(\leadsto\) \(\mathbf{a}\) is a local minimum
- \(AC - B^2> 0\) and \(A<0\) \(\leadsto\) negative definite \(\leadsto\) \(\mathbf{a}\) is a local maximum
- \(AC - B^2<0\) \(\leadsto\) indefinite \(\leadsto\) saddle point
- \(AC- B^2 = 0\) inconclusive
5.5 A simple optimization example
Suppose \(f:\Re^{2} \rightarrow \Re\) with
\[f(x_{1}, x_{2}) = 3(x_1 + 2)^2 + 4(x_{2} + 4)^2 \]
Calculate gradient:
\[ \begin{aligned} \nabla f(\mathbf{x}) &= (6 x_{1} + 12 , 8x_{2} + 32 ) \\ \mathbf{0} &= (6 x_{1}^{*} + 12 , 8x_{2}^{*} + 32 ) \end{aligned} \]
We now solve the system of equations to yield
\[x_{1}^{*} = - 2, \quad x_{2}^{*} = -4\]
\[ \textbf{H}(f)(\mathbf{x}^{*}) = \begin{bmatrix} 6 & 0 \\ 0 & 8 \\ \end{bmatrix} \]
\(\det(\textbf{H}(f)(\mathbf{x}^{*}))\) = 48 and \(6>0\) so \(\textbf{H}(f)(\mathbf{x}^{*})\) is positive definite. \(\mathbf{x^{*}}\) is a local minimum.
5.6 Maximum likelihood estimation for a normal distribution
Suppose that we draw an independent and identically distributed random sample of \(n\) observations from a normal distribution,
\[ \begin{aligned} Y_{i} &\sim \text{Normal}(\mu, \sigma^2) \\ \mathbf{Y} &= (Y_{1}, Y_{2}, \ldots, Y_{n} ) \end{aligned} \]
Our task:
- Obtain likelihood (summary estimator)
- Derive maximum likelihood estimators for \(\mu\) and \(\sigma^2\)
\[ \begin{aligned} L(\mu, \sigma^2 | \mathbf{Y} ) &\propto \prod_{i=1}^{n} f(Y_{i}|\mu, \sigma^2) \\ &\propto \prod_{i=1}^{N} \frac{\exp[ - \frac{ (Y_{i} - \mu)^2 }{2\sigma^2} ]}{\sqrt{2 \pi \sigma^2}} \\ &\propto \frac{\exp[ -\sum_{i=1}^{n} \frac{(Y_{i} - \mu)^2}{2\sigma^2} ]}{ (2\pi)^{n/2} \sigma^{2n/2} } \end{aligned} \]
Taking the logarithm, we have
\[l(\mu, \sigma^2|\mathbf{Y} ) = -\sum_{i=1}^{n} \frac{(Y_{i} - \mu)^2}{2\sigma^2} - \frac{n}{2} \log(2 \pi) - \frac{n}{2} \log (\sigma^2)\]
Let’s find \(\widehat{\mu}\) and \(\widehat{\sigma}^{2}\) that maximizes log-likelihood.
\[ \begin{aligned} l(\mu, \sigma^2|\mathbf{Y} ) &= -\sum_{i=1}^{n} \frac{(Y_{i} - \mu)^2}{2\sigma^2} - \frac{n}{2} \log (\sigma^2) \\ \frac{\partial l(\mu, \sigma^2)|\mathbf{Y} )}{\partial \mu } &= \sum_{i=1}^{n} \frac{2(Y_{i} - \mu)}{2\sigma^2} \\ \frac{\partial l(\mu, \sigma^2)|\mathbf{Y})}{\partial \sigma^2} &= -\frac{n}{2\sigma^2} + \frac{1}{2\sigma^4} \sum_{i=1}^{n} (Y_{i} - \mu)^2 \end{aligned} \]
\[ \begin{aligned} 0 &= -\sum_{i=1}^{n} \frac{2(Y_{i} - \widehat{\mu})}{2\widehat{\sigma}^2} \\ 0 &= -\frac{n}{2\widehat{\sigma}^2 } + \frac{1}{2\widehat{\sigma}^4} \sum_{i=1}^{n} (Y_{i} - \mu^{*})^2 \end{aligned} \]
Solving for \(\widehat{\mu}\) and \(\widehat{\sigma}^2\) yields,
\[ \begin{aligned} \widehat{\mu} &= \frac{\sum_{i=1}^{n} Y_{i} }{n} \\ \widehat{\sigma}^{2} &= \frac{1}{n} \sum_{i=1}^{n} (Y_{i} - \overline{Y})^2 \end{aligned} \]
\[ \textbf{H}(f)(\widehat{\mu}, \widehat{\sigma}^2) = \begin{bmatrix} \frac{\partial^{2} l(\mu, \sigma^2|\mathbf{Y} )}{\partial \mu^{2}} & \frac{\partial^{2} l(\mu, \sigma^2|\mathbf{Y} )}{\partial \sigma^{2} \partial \mu} \\ \frac{\partial^{2} l(\mu, \sigma^2|\mathbf{Y} )}{\partial \sigma^{2} \partial \mu} & \frac{\partial^{2} l(\mu, \sigma^2|\mathbf{Y} )}{\partial^{2} \sigma^{2}} \end{bmatrix} \]
Taking derivatives and evaluating at MLE’s yields,
\[ \textbf{H}(f)(\widehat{\mu}, \widehat{\sigma}^2) = \begin{bmatrix} \frac{-n}{\widehat{\sigma}^2} & 0 \\ 0 & \frac{-n}{2(\widehat{\sigma}^2)^2} \\ \end{bmatrix} \]
- \(\text{det}(\textbf{H}(f)(\widehat{\mu}, \widehat{\sigma}^2)) = \dfrac{n^2}{2(\widehat{\sigma}^2)^3} > 0\) and \(A = \dfrac{-n}{\widehat{\sigma}^2} < 0\) \(\leadsto\) maximum
- Determinant is greater than 0 and \(A\) is less than zero - local maximum
5.7 Computational optimization procedures
As the previous example suggests, analytical approaches can be difficult or impossible for many multivariate functions. Computational approaches simplify the problem.
5.7.1 Multivariate Newton-Raphson
Suppose \(f:\Re^{n} \rightarrow \Re\). Suppose we have guess \(\mathbf{x}_{t}\). Then our update is:
\[\mathbf{x}_{t+1} = \mathbf{x}_{t} - [\textbf{H}(f)(\mathbf{x}_{t})]^{-1} \nabla f(\mathbf{x}_{t})\]
- Approximate function with tangent plane
- Find value of \(x_{t+1}\) that makes the plane equal to zero
- Update again
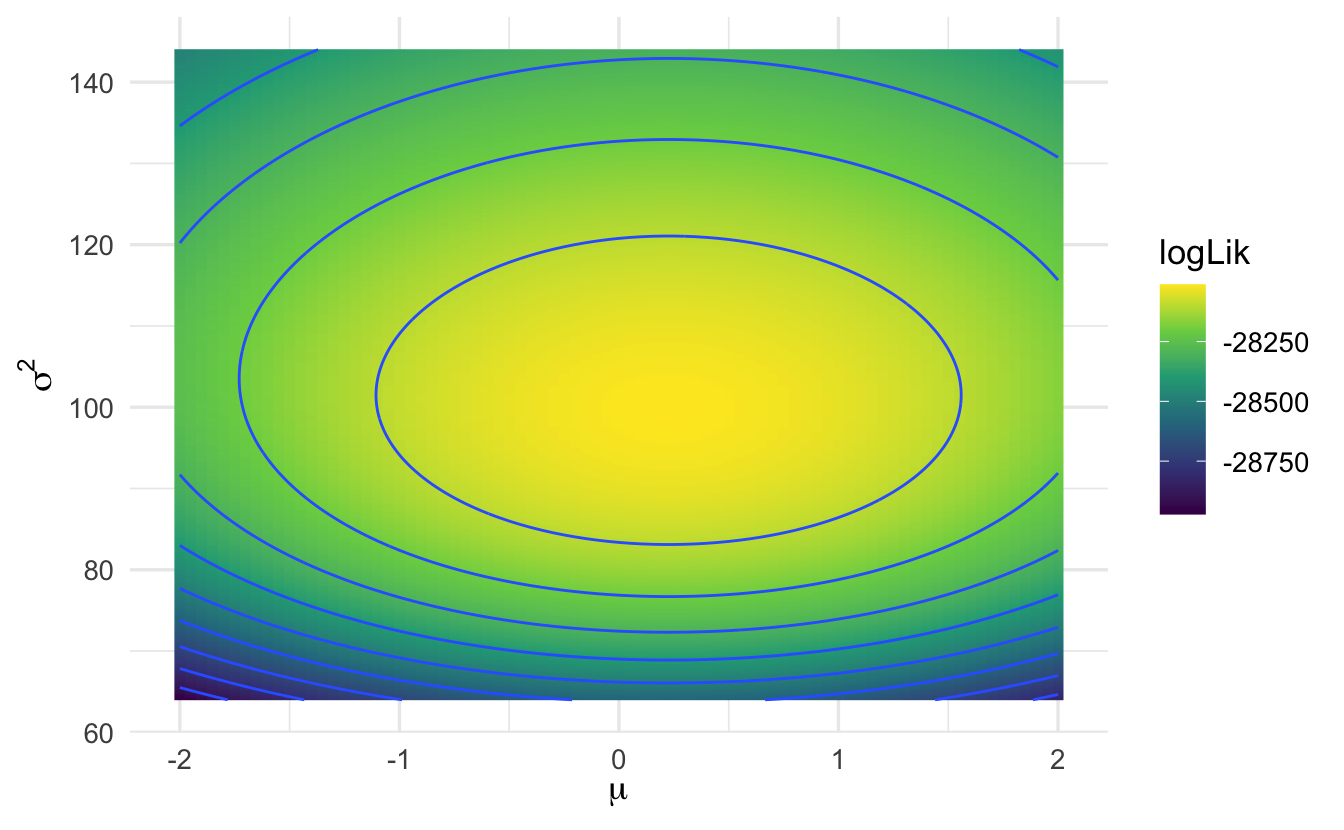
5.7.2 Grid search
- Example: MLE for a normal distribution
- In R, I drew 10,000 realizations from \(Y_{i} \sim \text{Normal}(0.25, 100)\)
- Used realized values \(y_{i}\) to evaluate \(l(\mu, \sigma^2| \mathbf{y} )\) across a range of values
- Computationally inefficient - have to try a large number of combinations of parameters
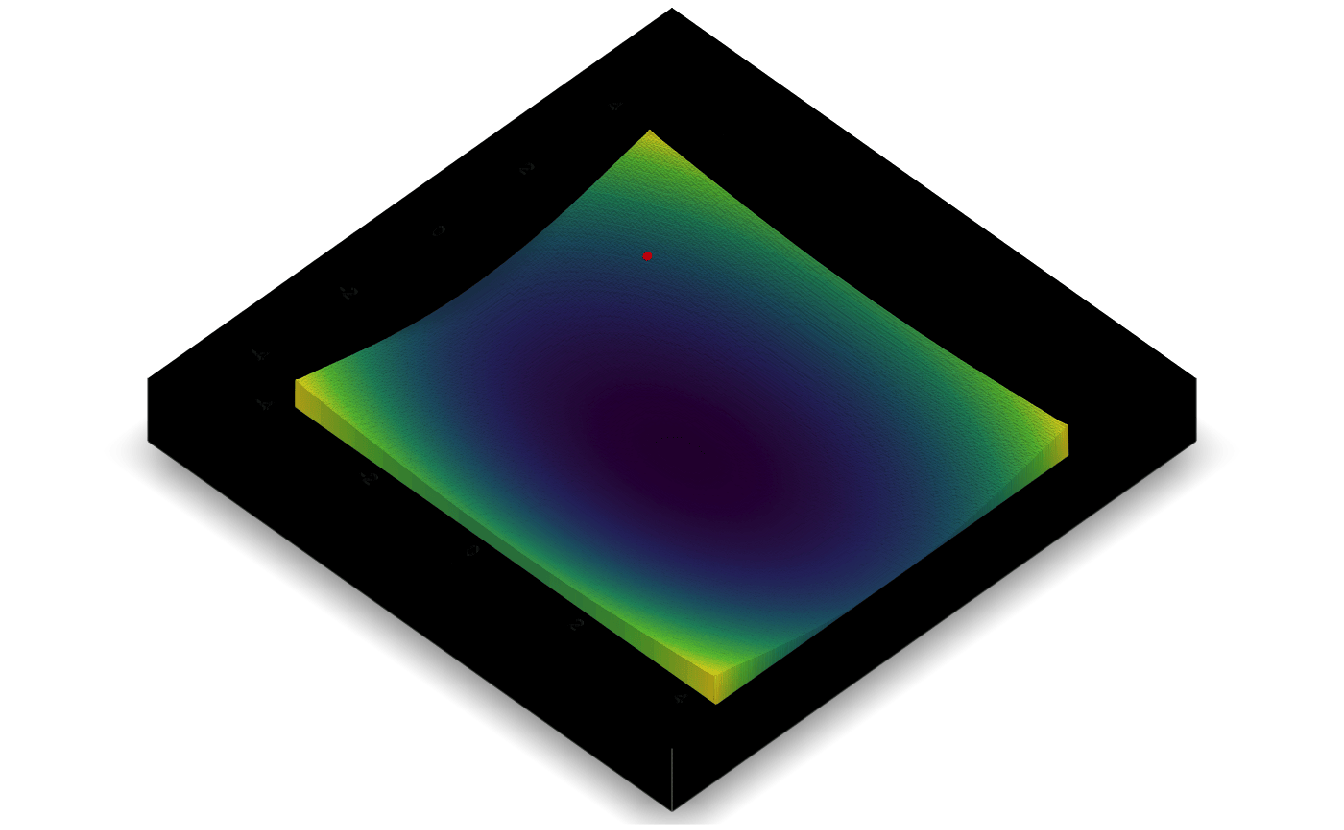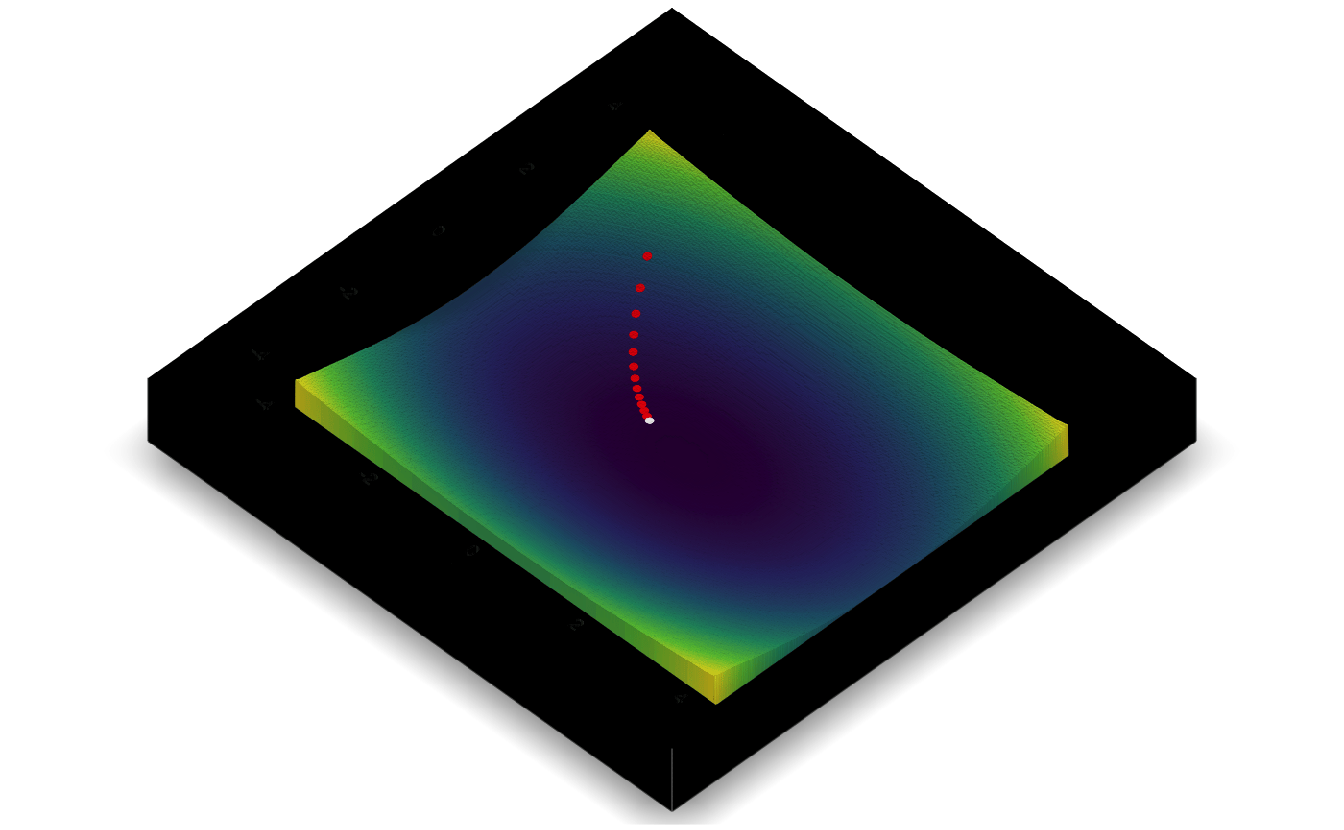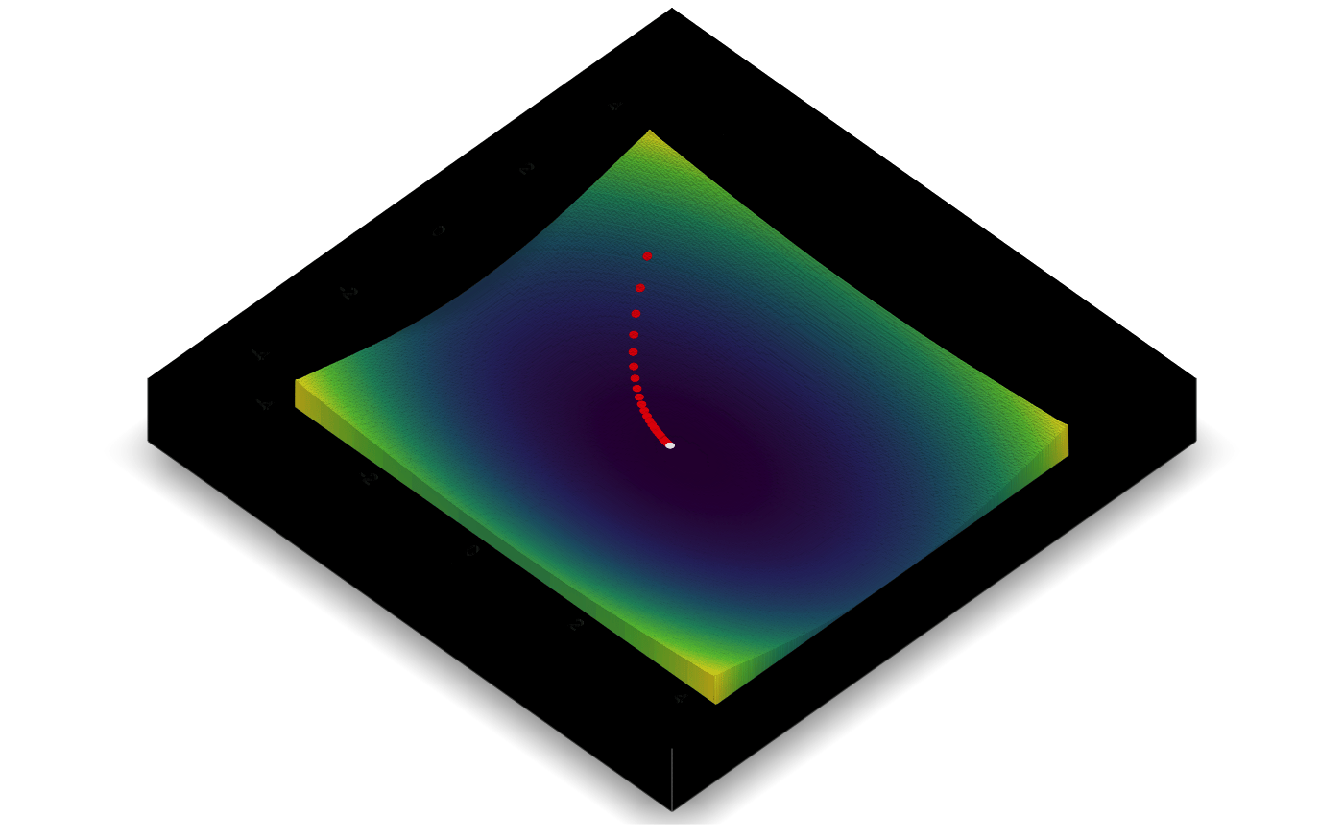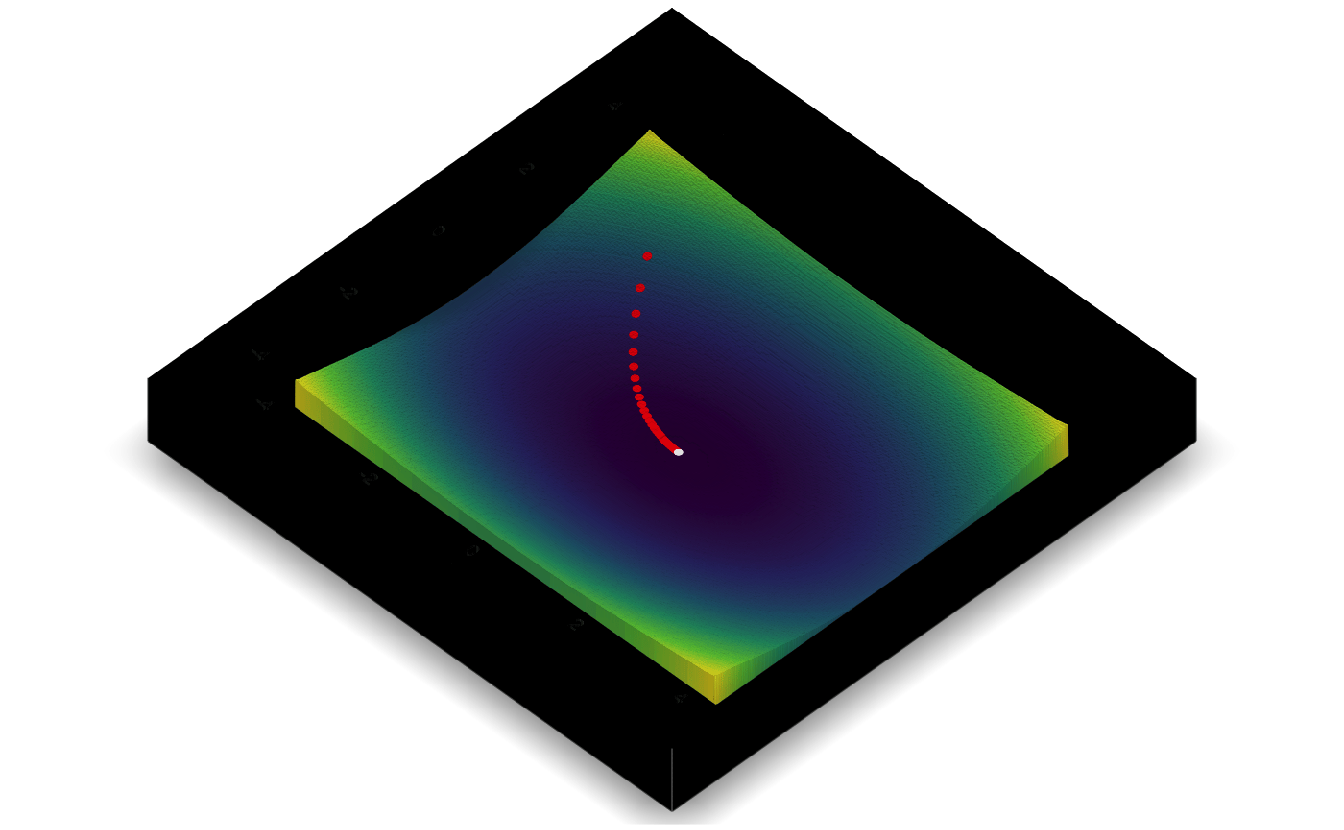
5.7.3 Gradient descent
Same approach as before, but now the derivative is a vector (i.e. gradient, hence the name of the approach “gradient” descent).
\[f(x, y) = x^2 + 2y^2\]